Regressão com scikit-learn

Fala galera do mundo dos dados, partiu regressão com scikit-learn! Antes de tudo este é o primeiro post da trilha de modelos de Machine Learning (ML) com sklearn, vamos começar com os mais básicos e evoluir até chegar em modelos mais complexos. Mas que raios são esses tais modelos? Modelos de ML são algoritmos com funções matemáticas treinados para reconhecer determinados padrões e realizar predições a partir desses padrões. Mas não é esse monstro todo que parece, vamos por partes igual ao Jack.

Neste post vamos abordar um dos modelos mais “básicos” de ML, mas não menos importante. A regressão linear apesar de um modelo relativamente simples, se comparado a outros que abordaremos nos próximos posts, tem um grande poder de predição e é solução para diversos problemas comuns. Antes de ver a sua aplicação com a biblioteca scikit-learn (uma das bibliotecas Python para análise de dados), vamos ver alguns conceitos importantes que não devem ser esquecidos. Partiu regressão com skearn!!!

Regressão linear

A regressão linear pode ser definida pela estatística como uma equação que busca estimar o(s) valor(es) de y, dados uma ou mais variáveis x. Sendo definido pela equação matemática:

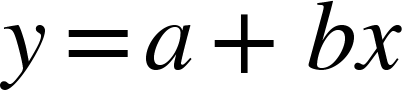
Assim y é a variável dependente de x, a é o coeficiente linear e b é o coeficiente angular. Mas calma que não é tão difícil quanto parece, na prática é bem mais simples, vamos em frente.

Curiosidades:

• Apesar do nome, a regressão linear também lida com relações não lineares.
• Em problemas de regressão, as variáveis independentes podem ser numéricas ou categóricas, enquanto a variável explicada (dependente) é sempre numérica.

Teoria

Então para deixar mais claro a nossa equação da regressão linear, vamos observar o gráfico abaixo. Logo podemos observar a variável a que vai definir o deslocamento da reta e a variável b que vai definir a inclinação da reta.

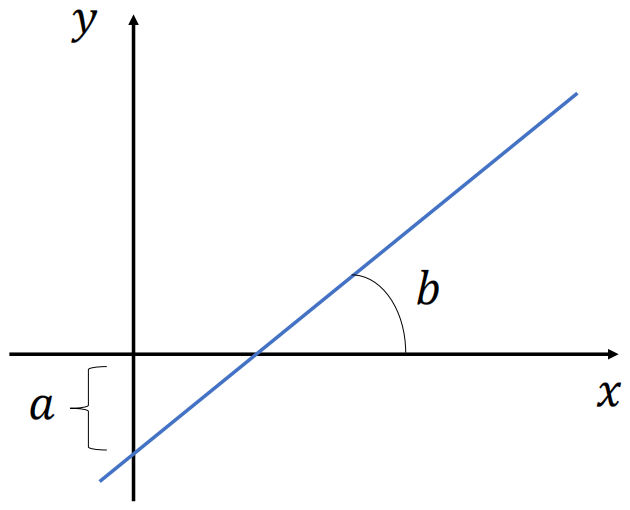
Alem disso, temos um exemplo onde a variável y é dependente de apenas uma variável x, mas nos problemas do mundo real, normalmente o que temos é a variável y dependente de várias variáveis x. Portanto temos a fórmula abaixo que representa mais de uma variável independente.

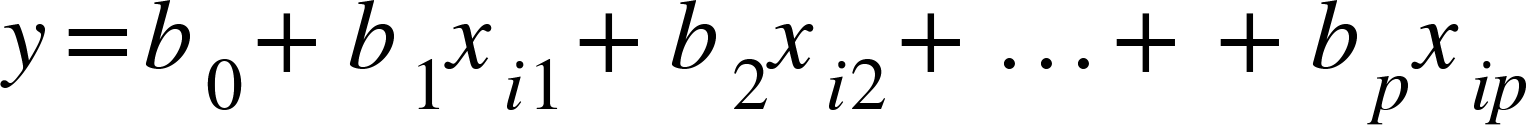
Ou seja vamos ter o número p de variáveis x, onde i denota a i-ésima observação do conjunto de treino. Mas não vamos nos preocupar com o tamanho da conta que o algoritmo vai fazer, para nós o importante agora é entender o conceito por trás da fórmula. Portanto, entendido o conceito vamos a um exemplo prático.

Regressão linear na Prática

Agora podemos Aplicar todos esses conceitos e fórmulas que vimos acima, para isso, vamos utilizar o python e sua poderosa biblioteca de algoritmos de aprendizado de máquina, a scikit-learn ou simplismente sklearn. Lá podemos encontrar o famoso dataset com os preço de casas em Boston (Boston house prices), disponível na própria biblioteca do scikit-learn através da função load_boston. Mas o que é o scikit-learn?

Essa biblioteca possui um conjunto de ferramentas para pré-processamento de dados e modelos de aprendizagem de máquina, inclusive a regressão linear, que se encontra no módulo linear_model, juntamente com outros modelos lineares. Mas vamos explorar todos os seus poderes especiais em diversos outros posts.

Sigamos em frente, com os dados desse dataset é possível, baseado nas suas features (variáveis independentes ou o x), fazer predições do target (variável dependente ou o y), neste problema o preço das casas em Boston.

Depois dessa introdução de alguns conceitos essenciais, vamos ao que interessa. Vamos pegar os dados desse dataset, dividi-lo em duas partes, uma parte vamos utilizar para treinar o modelo (vamos mostrar ao modelo um conjunto de dados com as entradas e saídas conhecidas) e a outra parte que até então desconhecida pelo modelo, vamos usar para testar (vamos mostrar ao modelo um conjunto de dados com as entradas para que ele faça uma predição das saídas), esse seria um modelo supervisionado, quando temos dados rotulados, nossa saída já é conhecida e usamos ela para treinar o modelo, já o modelo semi-supervisionado e o não supervisionado abordaremos em outros posts para não perder o foco. Aqui começamos a construção da regressão linear com scikit-learn.

Para começar vamos importar as bibliotecas necessárias para carga, tratamento e visualização dos dados, para criação do modelo e avaliação do mesmo.

Importando bibliotecas

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

Após carregar nossas bibliotecas, vamos carregar o nosso dataset para resolver nosso problema de regressão linear, nossos dados está dentro de uma das bibliotecas que foi carregada, o scikit-learn disponibiliza através do sklearn.datasets um conjunto de datasets para serem utilizados como exemplos e de lá selecionamos o load_boston, vamos ver agora como carregar ele.

Carregando dados do dataset de Boston

# Selecionando os dados do load_boston
boston = load_boston()
# Atribuindo as variáveis features, target, feature_names os seus valores correspondentes
features, target, feature_names = boston.data, boston.target, boston.feature_names
# Transformamos com o pandas esses dados em um DataFrame
df = pd.DataFrame(data=features, columns=feature_names)
# Juntamos ao DataFrame o target(y), nossa saida
df['PRICE'] = target
df.head(2)

Assim ao executar a função head() obtemos o seguinte resultado:

Visualizando dados

Vamos ter alguns posts específicos só para ensinar e dar dicas sobre a exploração de dados, uma parte fundamental para a criação do modelo, sem conhecer os dados fica complicado criar um modelo eficiente para o problema.

Mas vamos ver aqui duas funções clássicas do pandas(biblioteca open source utilizada para visualização e manipulação de dados):

• describe() – lista as variáveis e mostra alguns dados estatísticos básicos como (mínimo, máximo, média, e outros) não deixe de conferir o post sobre estatística para saber mais sobre esses dados (Estatística Descritiva Univariada).
• info() – lista informações sobre as colunas, utilizei para sabe se todas as features (x), nossas entradas eram numéricas e se não tinham dados nulos, pré requisitos para os modelos de regressão linear.

Após analisar estas funções podemos ir para nosso modelo de regressão linear. Só lembrando que estamos tratando do conceito da regressão linear, então pode parecer está faltando algumas etapas (como é um dataset de exemplo podemos pular algumas etapas para fins de demonstração, pois os dados já foram tratados) ná dúvida sobre as etapas dos projetos de ciência de dados pode conferir neste post (Pipeline dos Projetos de Ciência de Dados).

df.describe()

Assim ao executar a função describe() obtemos o seguinte resultado:

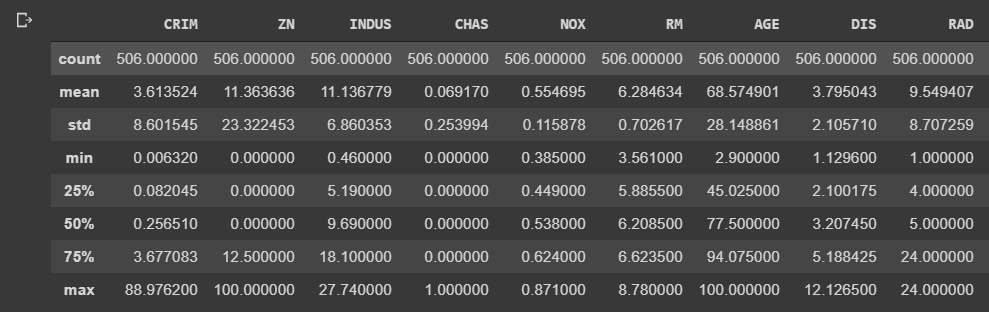
df.info()

Assim ao executar a função info() obtemos o seguinte resultado:

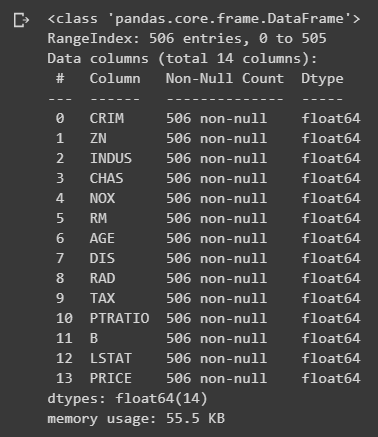
Modelo LinearRegression

Vamos começar selecionando nossas features e target, entradas e saídas ou simplesmente X e y são nomes comuns que podem aparecer na literatura. Para ficar mais didático vamos selecionar apenas uma variável de entrada.

Selecionando Variáveis para o modelo de regressão com scikit-learn

X = df[['LSTAT']]
y = df.PRICE

Após a seleção do X e y, como falado anteriormente, vamos dividir nossos dados em treino e teste para que possamos após a criação do modelo testar a performance do mesmo.

Dividindo os dados em treino e teste

O parâmetro test_size vai definir o tamanho dos nossos dados selecionados para teste, o tamanho dessa divisão, não existe uma regra para isso, vai depender de cada problema e principalmente do tamanho do conjunto de dados que temos para treino.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

Com nossos dados de treino dividido, podemos criar o modelo, que é uma tarefa relativamente simples, na prática o mais difícil é saber: Qual melhor modelo usar? Quais são os melhores hiperparâmetros? Mas essas e outras dúvidas vamos responder em outros posts.

Criando o modelo de regressão com scikit-learn

# Criando o modelo LinearRegression
regr = LinearRegression()
# Realizar treinamento do modelo
regr.fit(X_train, y_train)
# Realizar predição com os dados separados para teste
y_pred = lr.predict(X_test)
# Visualização dos 20 primeiros resultados
y_pred[:20]

Assim ao selecionar os 20 primeiros resultados da variável y_pred obtemos o seguinte resultado:

Lembra quando nós definimos a função da regressão linear?

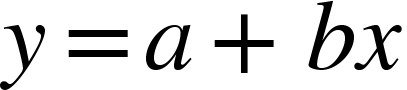
Abaixo nós temos o resultado de a o coeficiente linear e b o coeficiente angular do nosso modelo gerado, dados esses valores conseguimos prever qualquer ponto da reta somente com o valor de x, então temos o nosso modelo de regressão linear.

E agora? Terminamos? Nosso modelo ficou bom? Ainda precisamos avaliar nosso modelo afim de saber se ele resolve nosso problema com um erro aceitável. “Erro? Não pode ter erro.” Calma, os modelos são cálculos baseados em estatísticas então sempre vamos ter um erro, o que podemos fazer é minimizar este erro, para que ele seja aceitável para o nosso problema.

Validação de regressão linear com scikit-learn

Vejamos o gráfico abaixo, em azul nossa linha de regressão linear, em laranja nossas saídas originais, nosso erro é dado por e que é a diferença entre a saída original e a saída prevista pelo modelo, essa diferença pode ser positiva ou negativa e isso vai influenciar também na nossa análise de erro, vamos analisar o erro médio absoluto, o erro quadrático médio e o coeficiente de determinação.

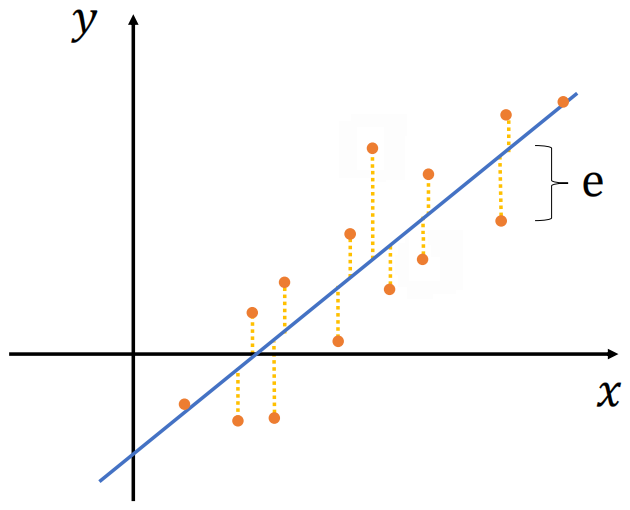
Erro Médio Absoluto (Mean Absolute Error)

O erro médio absoluto (MAE) é a média da soma de todos os e do nosso gráfico de erros, as sua análise sofre uma interferência devido aos erros positivos e negativos se anularem.

Para calcular o MAE do nosso modelo podemos usar o código abaixo.

print('MAE: %.2f' % mean_absolute_error(y_test, y_pred))

Assim ao executar o print() obtemos o seguinte resultado:

Erro Quadrado Médio (Mean Squared Error)

O erro quadrado médio (MSE) é a média da soma de todos os e elevados ao quadrado do nosso gráfico, o fato de ele ter as diferenças elevadas ao quadrados resolve o problema de os erros positivos e negativos se anulam, sendo mais preciso que o MAE.

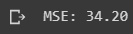
Para calcular o MSE do nosso modelo podemos usar o código abaixo.

print('Mean squared error: %.2f' % mean_squared_error(y_test, y_pred))

Assim ao executar o print() obtemos o seguinte resultado:

Coeficiente de Determinação (R2 Score)

O coeficiente de Determinação (R²) varia entre 0 e 1 e expressa a quantidade da variância dos dados que é explicada pelo modelo linear. Explicando a variância da variável dependente a partir da variável independente.

No nosso exemplo o R² = 0,56 significa que o modelo linear explica 56% da variância da variável dependente a partir da variável independente.

print('R2 Score: %.2f' % r2_score(y_test, y_pred))

Assim ao executar o print() obtemos o seguinte resultado:

Dada as explicações para avaliação do modelo, vamos visualizar os dados reais de forma gráfica para fixar os conhecimentos.

Visualizando os resultados da regressão linear com scikit-learn

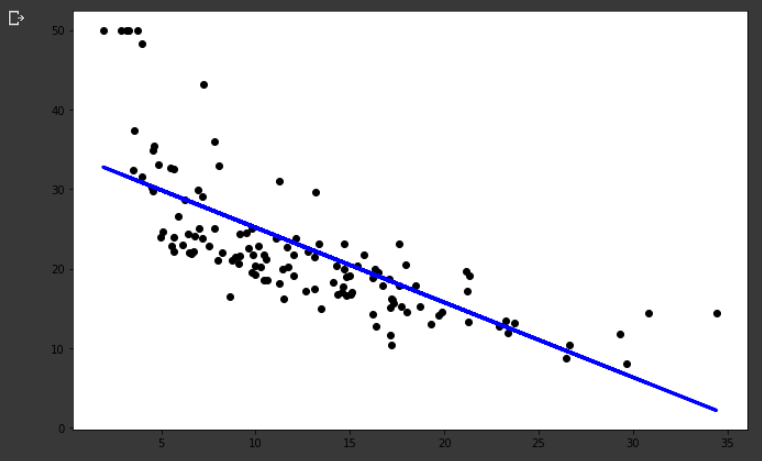
Podemos no gráfico abaixo, os pontos pretos que representam os nossos dados reais e em azul a reta de regressão linear do nosso modelo, dá para observar que temos dados um tanto dispersos, o que não faz o nosso modelos performar tão bem. Ao longo dos próximos posts vão entender melhor como melhorar nossos modelos, tratar os dados dispersos, incluir novas variáveis de entrada entre outras técnicas que podem ser aplicadas.

plt.scatter(X_test, y_test,  color='black')
plt.plot(X_test, y_pred, color='blue', linewidth=3)
plt.show()

Assim ao executar o plt.show() obtemos o seguinte resultado:

Como resultado do nosso trabalho vocês podem ter este exemplo completo, está disponível no nosso GitHub, confere lá: Regressão_Linear_com_scikit_learn.

Regressão com scikit-learn ao Cubo

Assim chegamos ao final deste post e este é o início da trilha de modelos de ML. Então, vamos começar devagar e ir subindo o nível a cada postagem. Sendo assim, no próximo post desta trilha vamos ver modelos de classificação com scikit-learn.

Portanto, espero ter atingido o objetivo de simplificar e abstrair para facilitar o entendimento de vocês sobre regressão linear com scikit-learn. Quero ouvir o feedback do que estão achando? O que podemos melhorar? O que tá faltando? É muito importante para a nossa evolução e trazer cada vez mais qualidades nos conteúdos.

Referências

• Introduction to Machine Learning Algorithms: Linear Regression
• Regressão linear
• Understanding Regression Error Metrics in Python

Conteúdos ao Cubo

Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.

• NLP com scikit-learn
• Classificação com scikit-learn
• Agrupamento com scikit-learn
• Previsão de Séries Temporais com SKTime
• Sistemas de Recomendações com Surprise
• Variáveis em Python
• Bases de Dados Gratuitas para Impulsionar suas Análises de Dados
• Web Scraping e Coleta de Dados Automatizada com Python

Finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades. 

Tiago Dias

Apaixonado por dados e tecnologia ❤️ , criando soluções com dados 📊 📈 , desde 2015, sempre buscando tornar os processos orientados! Com formação em Engenharia da Computação 💾 , MBA Gestão da Informação e Business Intelligence e Especialização em Data Science.

Também atuo como professor na área de dados. Nas horas vagas crio modelos de Machine Learning 🤖 com Python em desafios do Kaggle e escrevo no Dados ao Cubo sobre o mundo dos dados 🎲 !

Compartilhando conhecimentos sempre 🚀