Tudo bem galera?! Esperamos que sim! Hoje vamos falar de um assunto que parece não ser tão simples de entender, então vamos tentar simplificar as coisas. Vamos falar de matemática, mas calma sem susto! Ela não é tão complicada quanto parece, nosso papo de hoje é sobre Estatística Descritiva Univariada.
Mas que raios é esse negócio de estatística? E essa tal descritiva? Que treco é esse de univariada? Onde vivem?! De que se alimentam?!
O que é estatística?
Para a grande maioria das pessoas, inclusive eu a um tempo atrás, a estatística não passa daquele amontoado de tabelas, dados numéricos e informações passadas na televisão no jornal da noite, e estatístico era aquele cara que ficava coletando os dados e fazendo gráficos e tabelas.
Mas, na verdade, estatística vai muito além disso. A estatística é um conjunto de técnicas que permite, organizar, descrever, analisar e interpretar dados originários de estudos e/ou experimentos, realizados em qualquer área de atuação.
Primeiramente, vamos esclarecer resumidamente alguns conceitos da estatística:
- População: conjunto total das entidades sob análise. Normalmente não temos acesso a população num todo ou esse acesso é muito caro.
- Amostra: fatia perceptível da população que utilizaremos na análise.
- Estimadores: qualquer função matemática que tente estimar (prever) estatísticas da população a partir da amostra.
- Estimativas: Resultado numérico do emprego de um estimador em uma amostra.
Estatística Descritiva
A estatística descritiva tem a finalidade de descrever resumidamente a realidade observada (população ou amostra), usando métodos numéricos, gráficos e criando referências simples de maneira mais informativa possível.
Estatística Univariada
A Estatística Univariada compreende todos os mecanismos de Estatística Descritiva que possibilitam a análise de cada variável separadamente e também dispositivos de Estatística Inferencial para determinada variável, podendo esta ser medida para uma ou mais amostras independentes. A palavra “univariada” subentende que há apenas uma variável dependente (x é a variável independente e y a variável dependente).
Assim a análise univariada compreende explicar a distribuição de uma única variável, incluindo sua medida central (média, mediana e a moda) e sua dispersão (incluindo a diferença entre o maior e menor valor da amostragem e quantis do conjunto de dados, além da variância e desvio padrão). Calma, a gente chega lá.
Média
A média ou média aritmética, nada mais é do que a soma de todos os dados da amostra dividido pela quantidade de amostras. Assim temos a fórmula abaixo:
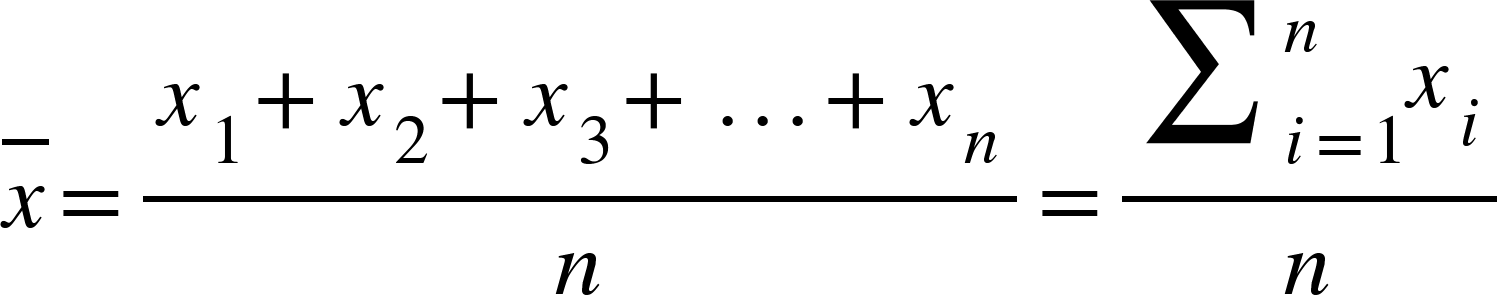
Vamos ver o exemplo com o seguinte conjunto X de dados:
X = {2, 4, 12, 54, 3}
Assim, podemos encontrar a média para o conjunto X aplicando a fórmula da média encontrando o resultado abaixo:
(2 + 4 + 12 + 54 + 3)/5 = 15
Mediana
Mediana (Md) é o valor representado pela amostra central, estando as amostras ordenadas em valores crescentes, caso o total de elementos for par, será necessário calcular a média dos dois valores centrais.
Vejamos os exemplos com os conjuntos de dados A e B abaixo:
A = {3, 1, 8}
B = {6, 4, 7, 2}
Vamos calcular a mediana para o conjunto A:
Ordenar o conjunto: A = {1, 3, 8}
O número de elementos é ímpar, então a mediana é o valor central: Md = 3
Vamos calcular agora a mediana para o conjunto B:
Ordenar o conjunto: B = {2, 4, 6, 7}
O número de elementos é par, então a mediana são os dois valores centrais dividido por 2: Md = (4 + 6)/2 = 5
Moda
A Moda (Mo) é o valor que aparece com mais frequência em um conjunto de dados, ou seja, o valor que se repete mais vezes. Para fazermos o cálculo da moda de um conjunto de dados, basta encontrar os dados que mais aparecem no conjunto.
Vejamos os exemplos para os conjuntos de dados A e B abaixo:
A = {2, 23, 4, 2, 5}
B = {17, 21, 2, 21, 8, 2}
Para o conjunto A, temos a moda: Mo = 2. É o número que mais aparece no conjunto.
Para o conjunto B, temos a moda é: Mo = 2 e 21. Que são os números que mais aparecem no conjunto. Então, podemos dizer que o conjunto B é bimodal (possui duas modas).
Variância
A variância é uma medida de dispersão dos dados, mede o quão afastados os dados estão da média. Quanto maior a variância, mais afastados os dados encontram-se da média. Assim temos a variância populacional (σ²), exemplificada pela fórmula:
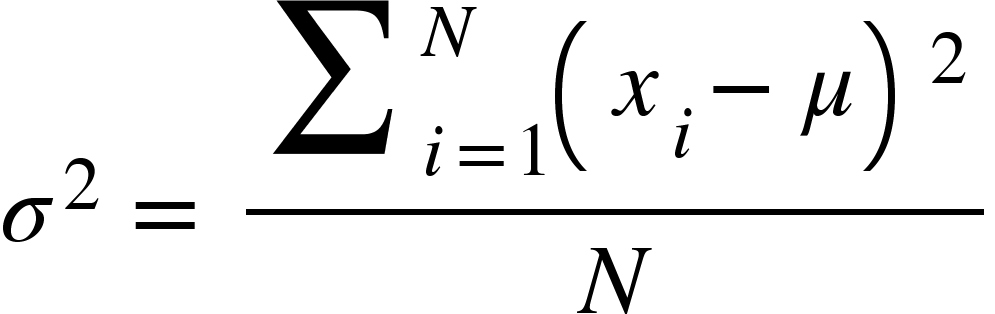
Onde N é o tamanho da população, Xi são os elementos da população e μ é a média populacional.
Assim também temos a variância amostral é dada por:
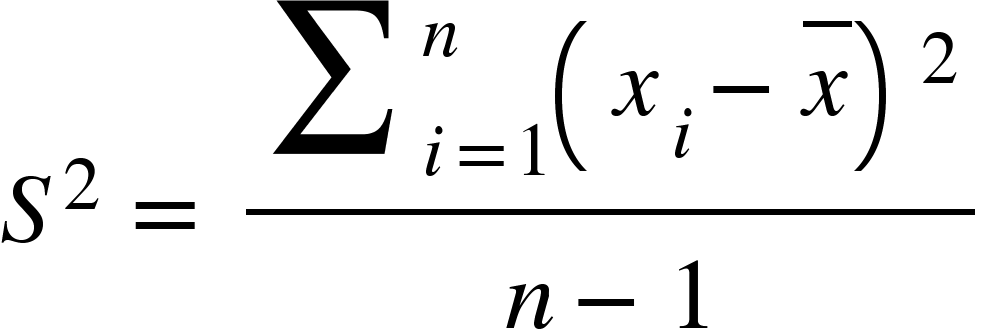
Mas qual motivo disso? Quando utilizamos a variância de uma amostra usando (n-1), a variância obtida será a melhor estimativa da variância da população. torna-se assim uma estimativa não tendenciosa e com menor erro médio.
Desvio padrão
O desvio padrão (standard deviation) é a raiz quadrada da variância. Toda discussão em relação à variância populacional Vs. amostral se aplica, com as devidas mudanças, ao desvio padrão. Podemos exemplificar o desvio padrão amostral (S) com a fórmula:
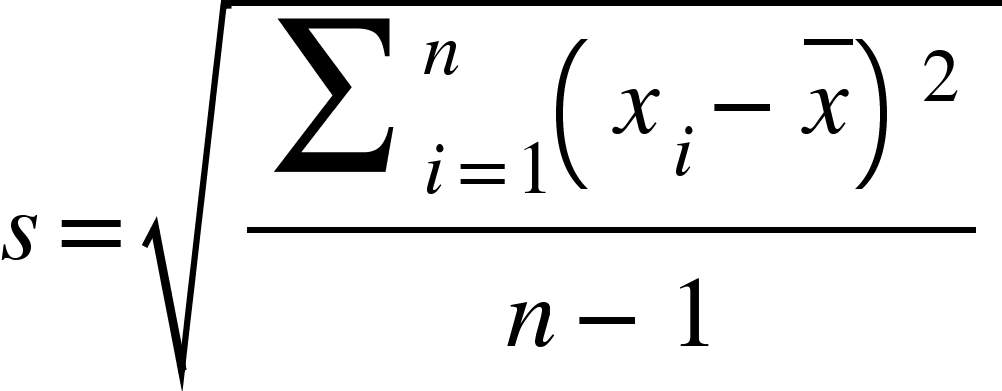
Quantil
Além da média, variância e desvio padrão, existem outras medidas de centralidade e dispersão dos dados univariadas que pode ser muito útil durante a análise exploratória dos dados conhecida também como EDA (Exploratory Data Analysis) uma dessas medidas é o quantil.
Quantis são pontos que dividem uma distribuição de probabilidade em partições de tamanhos iguais. Eles podem ser quartis (sendo o 1º quartil correspondente a 25% dos dados, o segundo quartil correspondente a 50% dos dados – a mediana e o 3º quartil correspondente a 75% dos dados) ou percentis (dividem a amostra em 100 partes).
Intervalo Interquartil (IQR)
O IQR (do inglês, Interquartile Range), é a diferença entre o terceiro e primeiro quartis: IQR = Q3−Q1. É uma medida de dispersão robusta muito utilizada, por exemplo, quando os dados contêm muitos outliers por ser menos sensível às variações nos extremos do conjunto.
Para verificar se há presença de outliers geralmente se utiliza o valor de 1.5*IQR ou 3*IQR. Outra forma de verificar seria utilizar a medida de 3 desvios padrões.
Assimetria (Skewness)
Assimetria é, na verdade, uma medida de simetria. Ela nos diz o quão simétrica é a distribuição dos dados em torno da média, e junto com a curtose (kurtosis) que veremos em seguida, é uma medida muito boa para informar a aparência ou forma da distribuição dos dados.
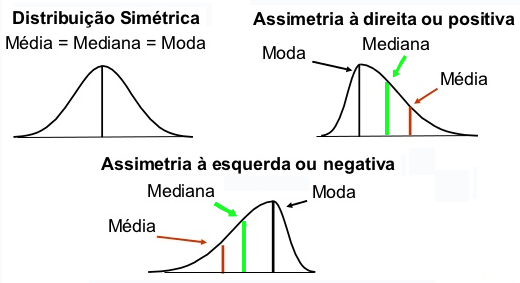
Valores zero da assimetria indicam que os dados têm distribuição simétrica em relação ao centro. Já valores positivos indicam que a distribuição tem assimetria positiva, ou seja, a cauda direita é mais longa do que a cauda esquerda. Por outro lado, valores negativos indicam que a distribuição tem assimetria negativa, ou seja, a cauda esquerda é mais longa do que a cauda direita. Podemos ver todas essas variações na figura abaixo:
Curtose (Kurtosis)
A Curtose ou achatamento também é uma medida que nos ajuda a dar forma à distribuição dos dados. A curtose, diferente da assimetria, tenta capturar em uma medida a forma das caudas da distribuição.
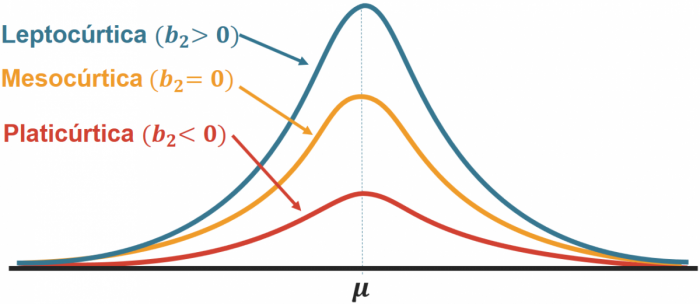
Temos basicamente três tipos de distribuição. A distribuição leptocúrtica, onde as caudas são mais pesadas e o pico da distribuição mais alto. A distribuição platicúrtica, onde as caudas são menos pesadas e a distribuição é mais achatada. E a mesocúrtica, quando se assemelha a distribuição normal.
Essa foi uma pequena abordagem sobre Estatística Descritiva Univariada, logo logo vamos apresentar aqui também a Análise Descritiva Multivariada, que é quando é analisada mais de uma variável ao mesmo tempo. Sendo assim, acompanhem nossas redes sociais para saber quando publicamos conteúdos novos! No mais, espero que tenham gostado, abraço a todos e até a próxima publicação!
Referências:
Média, moda e mediana
Estatística Descritiva
Para se aprofundar ainda mais no assunto:
Canal EstaTiDados
Thinks Stats
Estatística Prática Para Cientistas de Dados
An Introduction to Statistical Learning
Conteúdos ao Cubo
Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.
- Machine Learning com ML.Net no Jupyter Notebook
- Análise Exploratória com ML.Net e Jupyter Notebook no Ubuntu
- ML.Net – Modelos em Produção com WebApi e Docker
- AutoML (Automated Machine Learning) com ML.Net
- Analisando Dados do Brasileirão Série A
- Conceitos Iniciais do Python
- Bases de Dados Gratuitas para Impulsionar suas Análises de Dados
- Web Scraping e Coleta de Dados Automatizada com Python
Finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades.

Tudo sobre o universo Data Science!