Classificação com scikit-learn

Fala galera do mundo dos dados, partiu classificação com scikit-learn! Beleza? Antes de tudo, gostaria de saber de vocês o que estão achando dos nossos conteúdos! Tem alguma sugestão de conteúdo? Manda para nós. Quer ver seu artigo aqui no blog? Torne-se um Parceiro de Publicação D³. Sem mais delongas, hoje vamos falar sobre classificação com scikit-learn (uma das bibliotecas Python para análise de dados), este é mais um dos modelos de Machine Learning (ML) com sklearn. Vamos ver alguns conceitos importantes e como aplicar alguns algoritmos na prática. Partiu classificação com skearn!!!

Classificação

Os problemas de classificação são comuns e se resumem em uma tarefa de atribuição de classe dada uma observação de dados. Difícil ein? Classe? Observação? 

Vejamos, se temos um conjunto de dados ou dataset, cada exemplo que temos seria uma observação. Já a classe desse exemplo seria a classificação do mesmo. Por exemplo, se temos um conjunto de fotos de gatos e cachorros, e queremos fazer a classificação das fotos que são gatos. Cada foto será uma observação e a nossa classe será gato. Para resolver o nosso problema vamos classificar cada observação em positiva e negativa (O que vai ser positivo e negativo depende da narrativa do problema). Portanto temos uma classificação binária.

Mas poderia ter outro tipo de classificação? Claro, pegamos o mesmo problema acima e acrescentamos fotos de coelho. Assim, podemos ter um novo problema e queremos fazer a classificação por animal. Neste caso temos 3 classes de animais para fazer a classificação, gato, cachorro e coelho. Dessa forma teríamos uma classificação multiclasse.

Problema clássico de classificação

Dessa mesma forma vamos avaliar um problema clássico onde temos 3 espécies da flor íris para fazer sua classificação. De acordo com o nosso problema, temos algumas medidas das flores para fazer essa classificação.

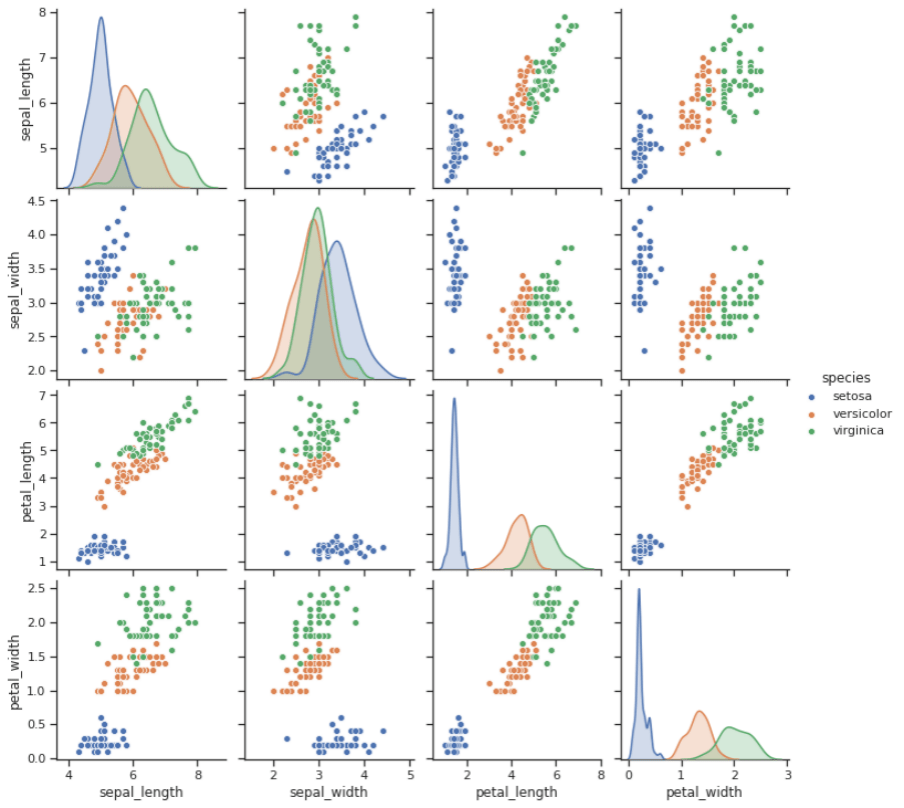
Na figura podemos ver as 4 características sendo analisadas em pares, através de gráficos de dispersão (através das coordenadas cartesianas para exibir valores de um conjunto de dados) e na diagonal principal histogramas (analisa a distribuição de frequências) de cada característica. Calma o detalhe de cada gráfico não é nosso foco de hoje, temos uma trilha completa aqui no Dados ao Cubo só para Exploração de Dados. 

De acordo com a figura podemos visualizar de uma forma gráfica como os nossos dados estão separados, e como vai ser possível classificar os mesmos. Mas esses são exemplos que já sabemos a classificação certo? E como vamos saber se nosso modelo está bom para classificar novos dados? Ótima pergunta, para isso vamos ver algumas formas de avaliação dos nossos modelos.

Avaliação de Modelos de Classiicação

Com a finalidade de avaliar modelos de classificação a matriz de confusão e curva ROC são instrumentos muito importantes. Dessa forma, vamos entender cada um desses avaliadores de desempenho dos classificadores. 

Matriz de confusão

A matriz de confusão é uma tabela que representa os acertos e erros de uma classificação. Dessa forma é possível fazer cálculos de performance através destes resultados obtidos como vamos ver a seguir.

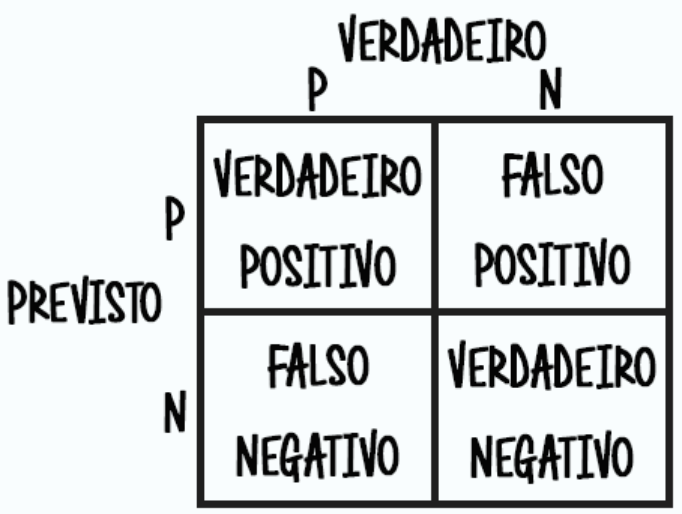
Antes de mais nada vamos entender alguns conceitos importantes dessa figura acima que representa uma matriz de confusão de um classificador binário. O que são os verdadeiros positivos e negativos? O que são os falsos positivos e negativos?

Os verdadeiros positivos e negativos nada mais são que os acertos do classificador. Os falsos positivos e negativos são erros do classificador. O falso positivo é quando o classificador aponta como positivo mas o correto seria negativo, ou seja erro TIPO 1. O falso negativo é quando o classificador aponta negativo mas o correto seria positivo, ou seja erro do TIPO II. 

Entendido os conceitos da matriz de confusão e seus possíveis erros podemos seguir para os cálculos de performance. 

• Acurácia – A acurácia é a proporção das observações classificadas corretas dentre o total de observações.
• Precisão – A precisão é a proporção das observações positivas classificadas corretamente dentre as observações positivas que foram previstas.
• Recall – O recall é a proporção das observações positivas classificadas corretamente dentre as observações positivas verdadeiras.
• F1 Score – O F1 Score é a média harmônica entre precisão e recall.

Juntamente com a matriz de confusão, vamos analisar agora a curva ROC para avaliação dos classificadores.

Curva ROC

A Curva Característica de Operação do Receptor (Receiver Operating Characteristic Curve), ou, simplesmente, curva ROC é uma representação gráfica do desempenho do classificador. Assim vamos ver abaixo uma figura para auxiliar no entendimento desse conceito.

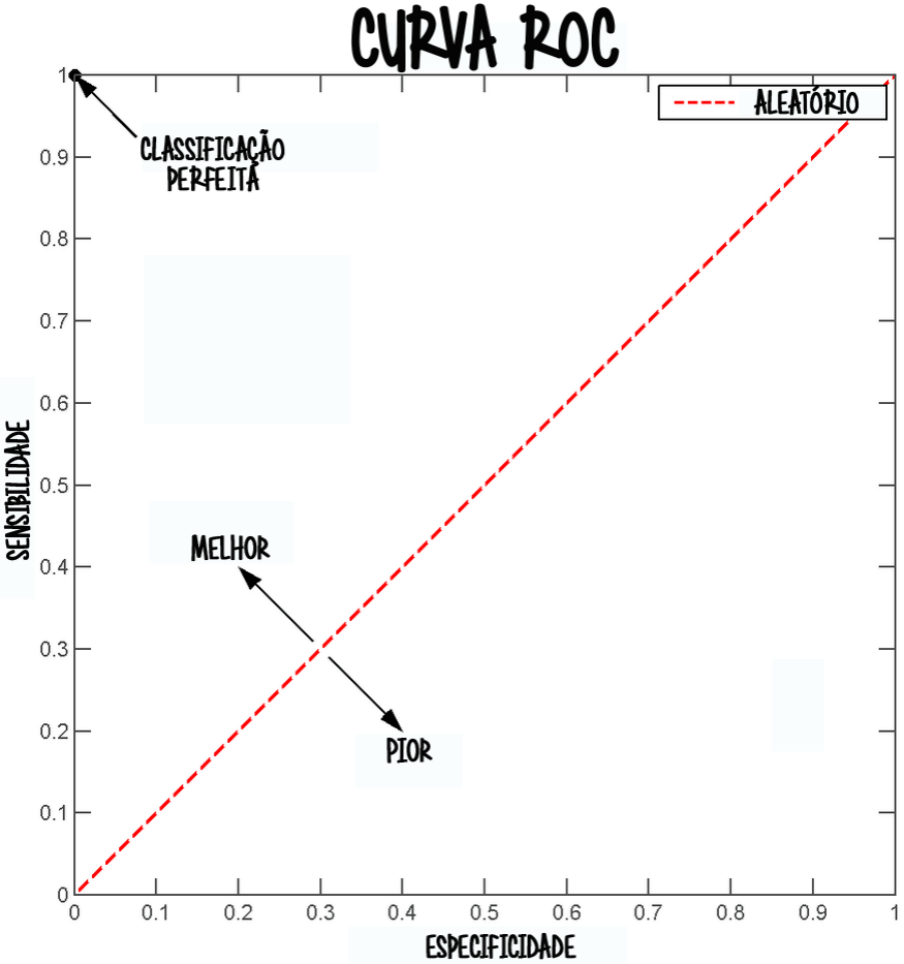
Em um mundo ideal (que não acontece na realidade) a curva ROC deveria estar na CLASSIFICAÇÃO PERFEITA. Acertar todas as observações positivas em 100% (recall = 1) e nunca classificar errado uma observação negativa.

Mas no mundo real, com problemas reais, basta a curva ROC estar acima do limite ALEATÓRIO que já temos algo satisfatório. Qualquer ponto seguindo a seta MELHOR é bom? Não é bem assim também, a avaliação de performance depende de cada problema e isso é muito relativo. A curva ROC bem como a matriz de confusão e suas métricas servem para ajudar a se aproximar do modelo ideal para aquele problema.

“Mas eu fiz as avaliação acimas com resultados muito bons e quando apresentei novos dados não funcionou!!!???” Calma, nem tudo está perdido, pode ser um problema de desbalanceamento dos dados. A seguir vou te mostrar como identificar esse problema e possíveis soluções.

Desbalanceamento em Modelos de Classificação

Um problema muito comum em problemas de classificação é ter uma classe sendo minoritária, ou seja, ela representa a minoria naquela conjunto de observações.

Por exemplo, temos um classificador que identifica se uma foto é gato ou não em um conjunto de fotos de animais. Porém no nosso conjunto de fotos 97% são fotos de gatos e apenas 3% são outros animais (não gatos). Os classificadores entendem, de forma equivocada, que se ele prever todas as fotos como gato ele vai acertar em 97% das vezes. Gerando uma falsa avaliação de bom desempenho.

Como resolver esse problema? É possivel?

Portanto precisamos balancear os dados antes de fazer a classificação. As técnicas mais comuns são através de reamostragem (resampling). Podendo ser feito basicamente de duas formas:

• Undersampling: Remover dados da classe majoritária;
• Oversampling: Reamostrar dados da classe minoritária;

Vamos ver a técnica SMOTE (Synthetic Minority Oversampling Technique), uma forma de oversampling que adiciona dados sintéticos da classe minoritária ao conjunto de dados. Vamos ver também a técnica NearMiss, uma forma de undersampling que remove dados da classe majoritária.

SMOTE

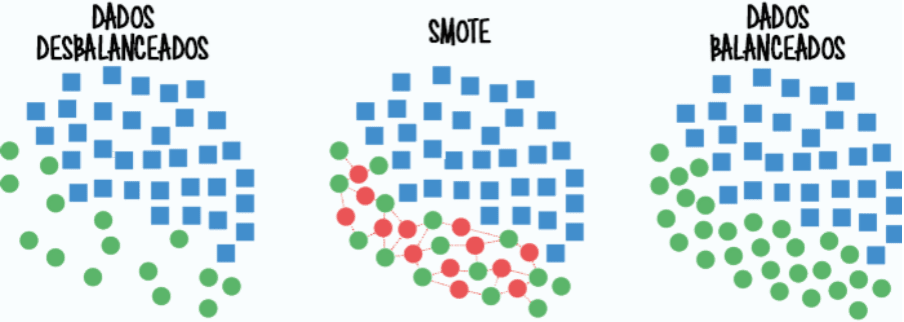
Uma das formas possíveis de corrigir o desbalanceamento dos dados é criar dados sintéticos similares aos dados originais, em outras palavras fazer oversampling. 

No nosso exemplo dos gatos, seria criar dados sintético a partir das fotos dos outros animais até o nosso conjuntos de dados ficar balanceado. Podemos ver na figura abaixo como seria esse processo com a técnica SMOTE.

NearMiss

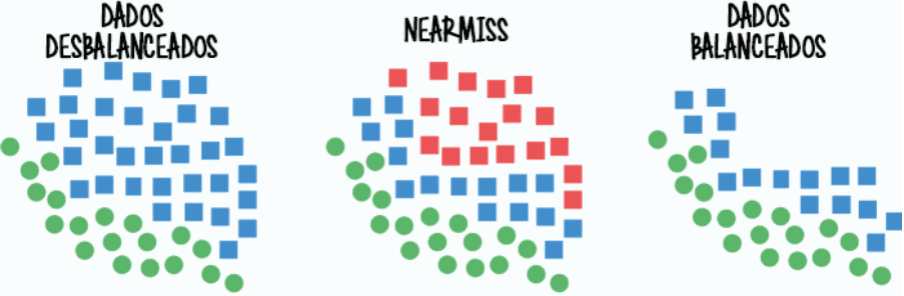
Uma outra formas possíveis de corrigir o desbalanceamento dos dados é remover dados da classe com maior quantidade de dados, em outras palavras fazer undersampling. 

No nosso exemplo dos gatos, seria remover fotos dos gatos até o nosso conjuntos de dados ficar balanceado. Podemos ver na figura abaixo como seria esse processo com a técnica NearMiss.

Agora que já entendemos os problemas de classificação, sabemos como avaliar, e também tratar problemas de balanceamento dos dados podemos entender alguns algoritmos da nossa conhecida biblioteca scikit-learn que podem aprender e classificar novos dados. Vamos ver como implementar isso com o python.

Classificação com sklearn Python

Para começar a criar nossos modelos de classificação com sklearn em python, precisamos importar as bibliotecas, vejamos o código no python. Após a biblioteca importada vamos carregar o nosso dataset, selecionar as variáveis de entrada e saída e dividir nosso dados em treino e teste para poder avaliar o modelo. Vamos ver esse 4 passos abaixo, a fim de resolver nosso problema de classificação que é identificar a espécie de uma flor dada algumas características de entrada:

Importar bibliotecas

import pandas as pd
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report

Selecionar dataset

df = sns.load_dataset("iris")

Podemos selecionar os nossos dados de algumas fontes, hoje escolhi selecionar através da função load_dataset(). Esta função está disponível na biblioteca gráfica seaborn, que além de ter os gráficos mais bonitos, ainda tem vários exemplos para que possamos fazer nossos testes. Portanto vamos selecionar um conhecido dataset de estudo o iris.

Selecionar variáveis de entrada e saída

X = df.drop(columns='species')
y = df.species

Para as variáveis de entrada vamos selecionar todas as características da flor, ou seja, toda a nossa dimensionalidade (são os atributos dos dados), neste exemplo temos 4. E a nossa saída será a espécie da flor.

Definir dados de treino e teste

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7)

O tamanho dos dados selecionados para teste foi de 70% para fins didáticos, devido ao fato do dataset ser de estudo e os dados treinados com mais do que isso deixa as avaliações quase sem erros. Essa divisão vai sempre depender de cada problema.

Agora vamos seguir para nossos modelos e a avaliação dos mesmos

Modelo de Classificação Regressão logística

Regressão logística? Mas não estávamos falando sobre classificação? Sim claro, apesar do nome regressão é um algoritmo para problemas de classificação. A regressão logística estima probabilidades para uma observação de acordo com a(s) variável(eis) explicativa(s), ou seja, nossa(s) variável(eis) de entrada. Confere a imagem abaixo.

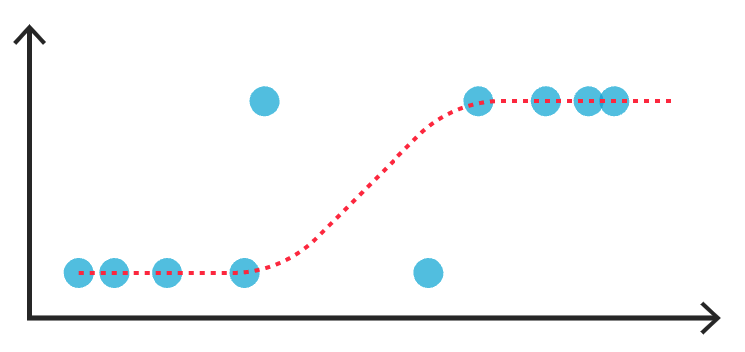
Por exemplo, no modelo de classificação com scikit-learn, vamos utilizar o modelo de LogisticRegression().

Regressão logística com sklearn Python

# Criando modelo e treinando com os dados de treino
clr = LogisticRegression()
clr.fit(X_train, y_train)
# Fazendo a predição nos dados de treino
resultado_clr = clr.predict(X_test)

Aqui está a criação modelo de regressão logística, o treinamento e a predição do modelo. Agora vamos ver como avaliar esse modelo.

Avaliação da regressão logística com Python

# Principais métricas de performance
print(classification_report(y_test, resultado_clr))

             precision    recall  f1-score   support

      setosa       1.00      1.00      1.00        32
  versicolor       0.87      1.00      0.93        33
   virginica       1.00      0.88      0.93        40

    accuracy                           0.95       105
  	macro avg      0.96      0.96      0.95       105
weighted avg       0.96      0.95      0.95       105

A função classification_report() disponível nas métricas do scikit-learn trás as principais métricas de performance para modelos de classificação. Como vimos no item 2.1 os 4 principais indicadores de performance acurácia, precisão, recall e o F1 score. Agora vamos ver a matriz de confusão e a curva ROC para o modelo de regressão logística.

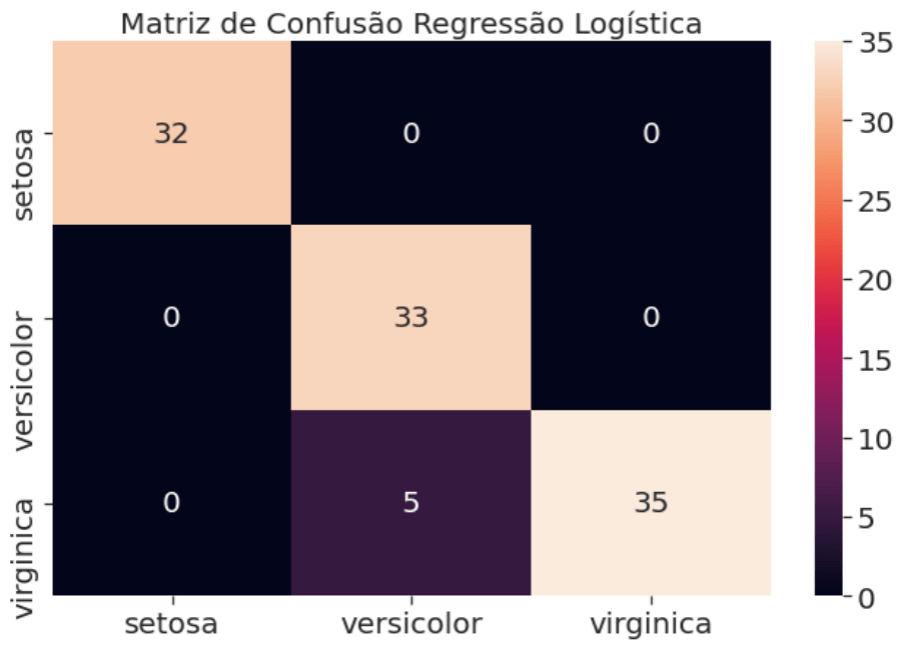
Para completar a nossa avaliação a nossa matriz de confusão, uma forma visual para ver os erros e acertos do nosso classificador.

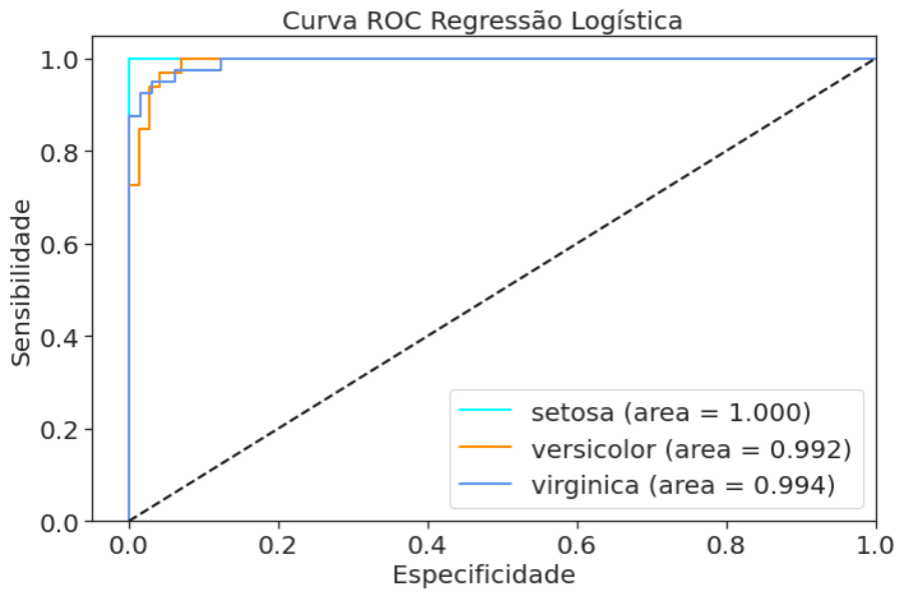
E a cereja do bolo, a curva ROC para finalizar a avaliação do nosso modelo, que podemos ver com todas as métricas até aqui está excelente. Mas não se engane o dataset para estudo os dados estão “quase perfeitos”, muito diferente da vida real.

O próximo algoritmo de classificação é o kNN, vamos entender como ele funciona.

Modelo de Classificação K Nearest Neighbors (KNN)

Já o algoritmo do KNN (como é mais conhecido), ou k-vizinhos mais próximos se traduzido, ele busca estimar o valor de uma classe observando os pontos mais próximos. Por padrão essa distância é calculada a distância euclidiana que explicamos no post (Geometria Analítica com SymPy), mas pode também ser calculadas com outras medidas. Vejamos a figura para melhorar o entendimento do KNN.

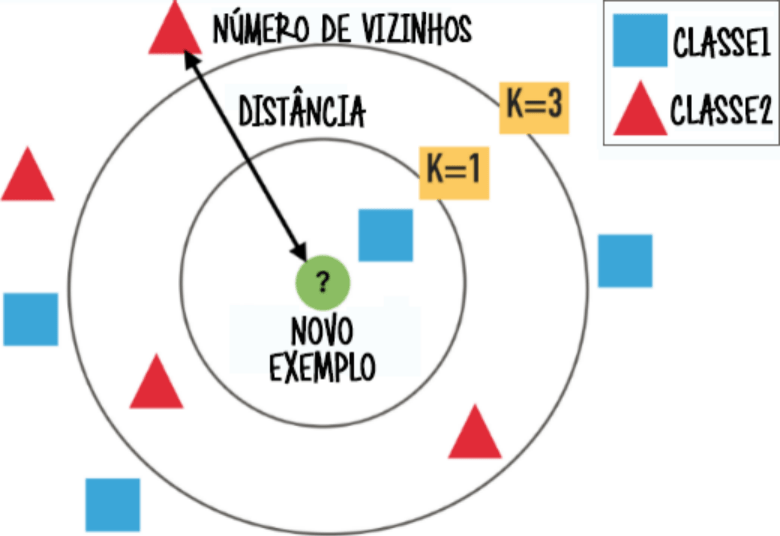
A ? representa o nosso NOVO EXEMPLO que vamos classificar, quadrados azuis são a CLASSE1 e triângulos vermelhos são a CLASSE2. Então temos a DISTÂNCIA para os pontos mais próximos e o NÚMERO DE VIZINHOS que vão ser levados em consideração para classificar. Caso o algoritmo seja configurado como K=1 o NOVO EXEMPLO seria classificado como quadrado azul, mas se for configurado como K=3 o NOVO EXEMPLO seria classificado como triângulo vermelho. Portanto dá para perceber como uma sutil mudança que pode fazer toda a diferença.

Mas Tiago, existe o número de K perfeito? Claro que NÃO, vai depender de cada problema, e a avaliação do modelo vai definir o melhor valor para K.

Agora vamos para o modelo de classificação com scikit-learn usando a função KNeighborsClassifier().

KNN com sklearn Python

# Criando modelo e treinando com os dados de treino
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
# Fazendo a predição nos dados de treino
resultado_knn = knn.predict(X_test)

Aqui está a criação modelo KNN, o treinamento e a predição do modelo. Agora vamos ver como avaliar esse modelo.

Avaliação do KNN com Python

# Principais métricas de performance
print(classification_report(y_test, resultado_knn))

             precision    recall  f1-score   support

      setosa       1.00      1.00      1.00        32
  versicolor       0.97      0.94      0.95        33
   virginica       0.95      0.97      0.96        40

    accuracy                           0.97       105
	macro avg      0.97      0.97      0.97       105
weighted avg       0.97      0.97      0.97       105

A função classification_report() disponível nas métricas do scikit-learn trás as principais métricas de performance para modelos de classificação. Agora vamos ver a matriz de confusão e a curva ROC para o modelo knn.

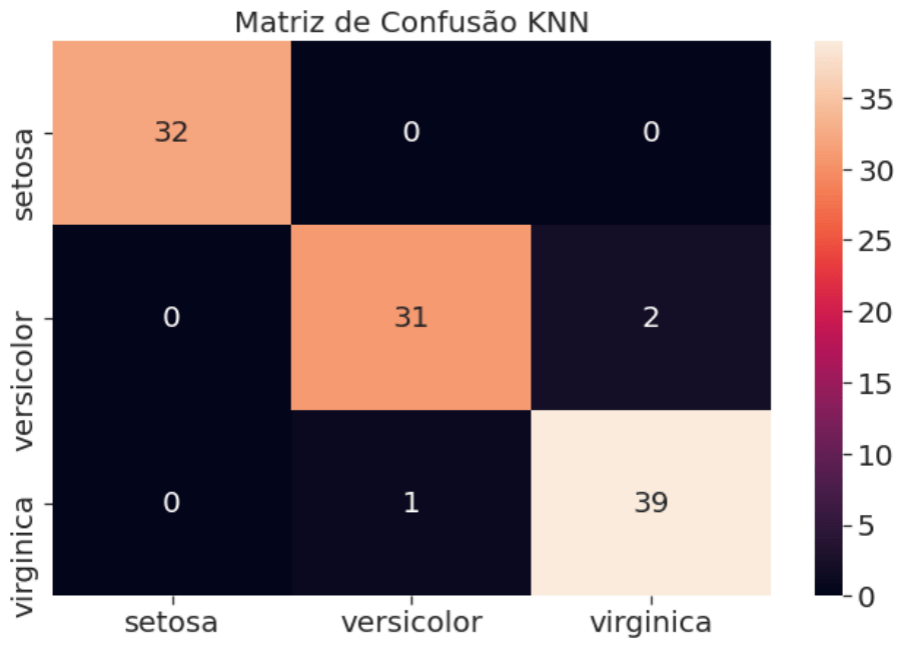
Para completar a nossa avaliação a nossa matriz de confusão, uma forma visual para ver os erros e acertos do nosso classificador.

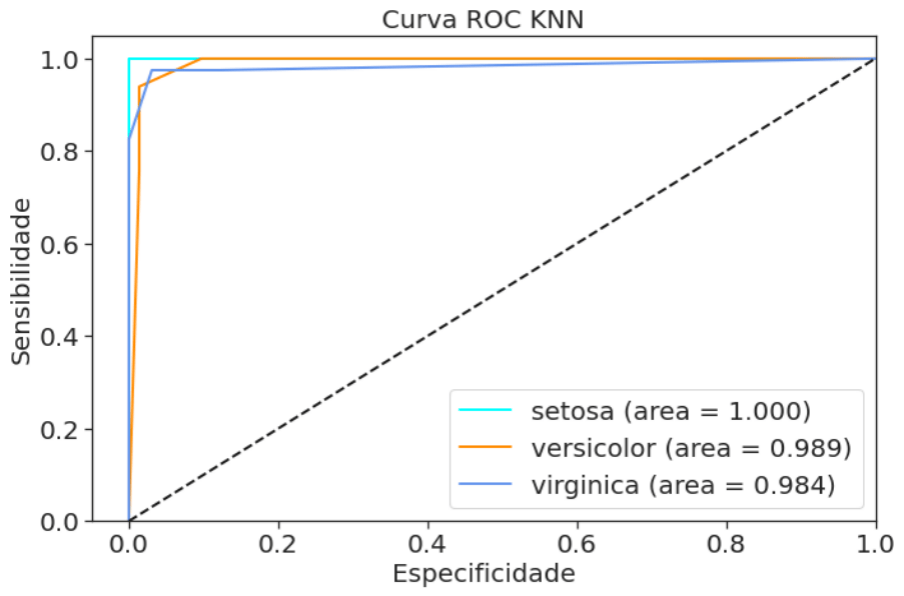
E a ameixa do bolo, a curva ROC para finalizar a avaliação do nosso modelo, que podemos ver com todas as métricas até aqui e comparado aos outros modelos seria também uma boa opção.

Por fim, o nosso último algoritmo de classificação dehoje a árvore de decisão, vamos ver como ela funciona.

Modelo de Classificação Árvores de decisão

Para finalizar nossos algoritmos hoje, a árvore de decisão, que funciona realmente como uma árvore. Cada galho da árvore se divide em dois até chegar às folhas, que são as decisões da árvore. Vamos ver a figura a seguir para fixar o entendimento.

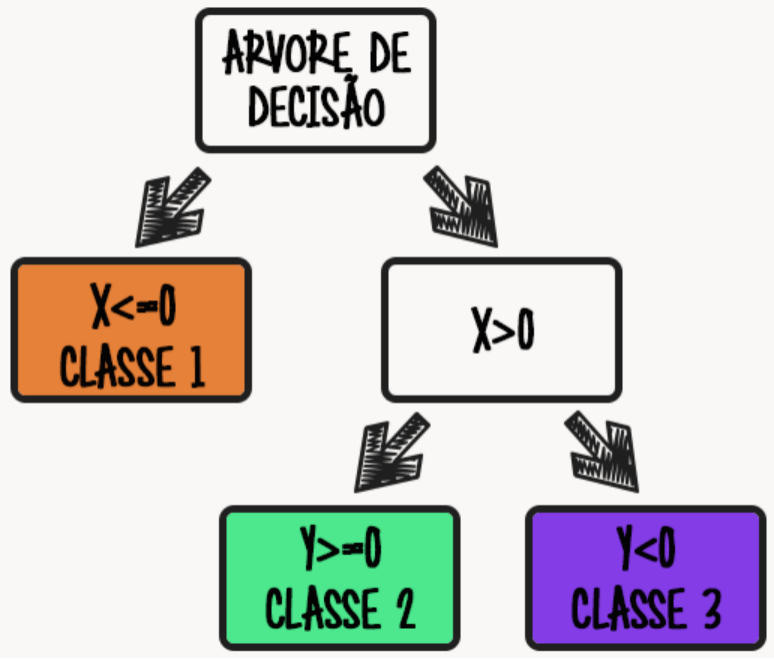
No exemplo figurado acima, temos duas variáveis de entradas e três classes possíveis como saída. Primeiramente o algoritmo verifica a variável X, caso ela seja menor ou igual a 0 a saída é CLASSE 1. Se a variável X for maior que 0, ele verifica a segunda variável, caso Y seja maior ou igual a 0 a saída é CLASSE 2, mas se Y for menor que 0 a saída será CLASSE 3. Portanto vimos neste simples exemplo de uma forma ilustrada o funcionamento do algoritmo.

Mas agora vamos ver o funcionamento de uma árvore de classificação com scikit-learn usando a função DecisionTreeClassifier().

Árvore de decisão com sklearn Python

# Criando modelo e treinando com os dados de treino
dtc = DecisionTreeClassifier()
dtc.fit(X_train, y_train)
# Fazendo a predição nos dados de treino
resultado_dtc = dtc.predict(X_test)

Aqui está a criação modelo KNN, o treinamento e a predição do modelo. Agora vamos ver como avaliar esse modelo.

Avaliação da árvore de decisão com Python

# Principais métricas de performance
print(classification_report(y_test, resultado_dtc))

             precision    recall  f1-score   support

      setosa       1.00      1.00      1.00        32
  versicolor       0.74      0.97      0.84        33
   virginica       0.97      0.72      0.83        40

    accuracy                           0.89       105
  	macro avg      0.90      0.90      0.89       105
weighted avg       0.91      0.89      0.89       105

A função classification_report() disponível nas métricas do scikit-learn trás as principais métricas de performance para modelos de classificação. Agora vamos ver a matriz de confusão e a curva ROC para o modelo da árvore de decisão.

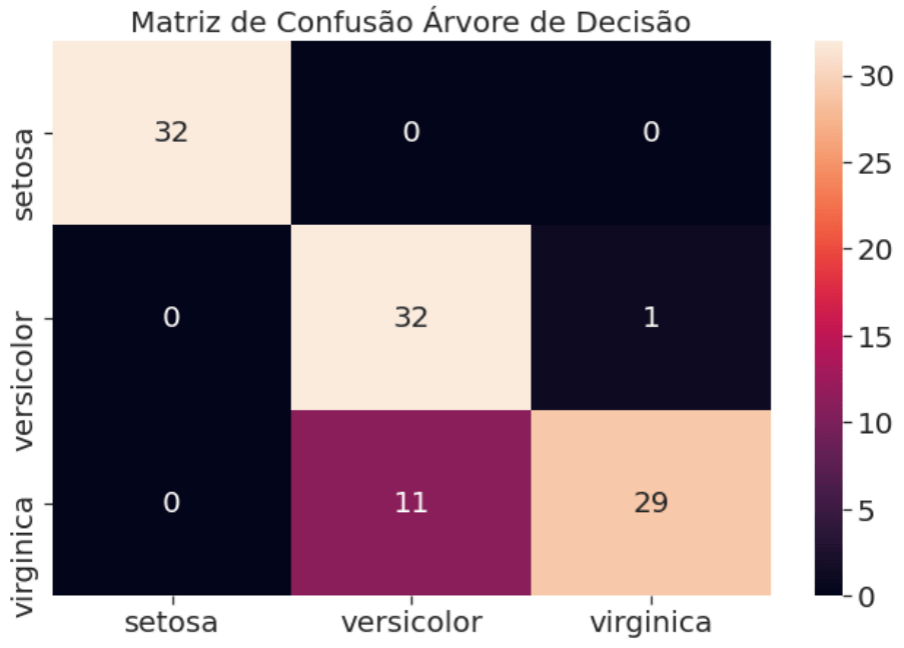
Para completar a nossa avaliação a nossa matriz de confusão, uma forma visual para ver os erros e acertos do nosso classificador.

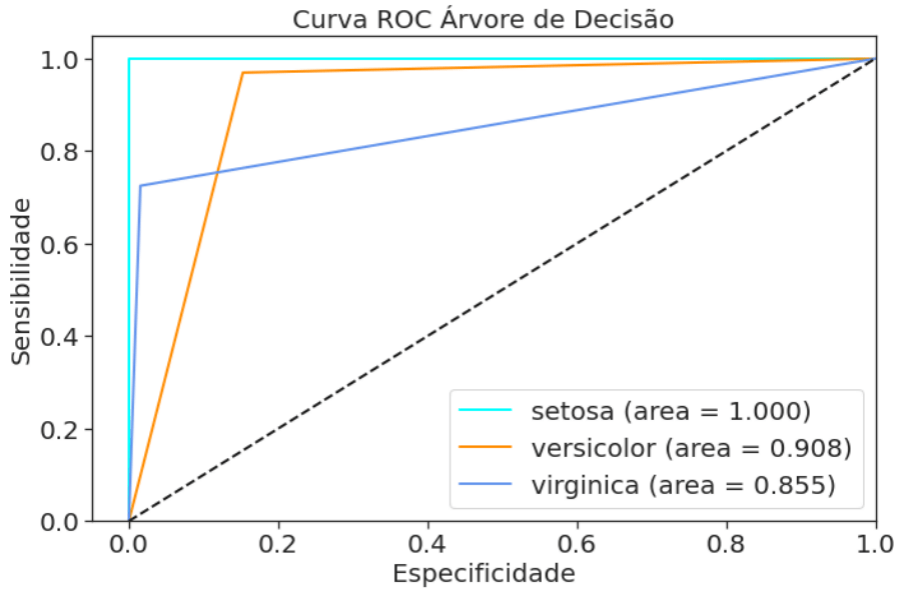
E o morango do bolo, a curva ROC para finalizar a avaliação do nosso modelo, que podemos ver com todas as métricas até aqui e comparado aos outros modelos não foi o melhor algoritmo para este problema.

Classificação com scikit-learn ao Cubo

Enfim chegamos ao final, apesar de longo espero que goste do conteúdo. Vimos hoje uma forma de resolver problemas de classificação com Python e a biblioteca scikit-learn, mas existem outras bibliotecas que dão outras possibilidades de resolver esse e outros problemas de classificação. Nesse sentido vimos como avaliar os modelos criado e ver também que os diferentes modelos aplicados para o mesmo conjunto de dados podem trazer resultados diferentes. Dessa forma reforça o que sempre falamos: que a análise depende de cada problema. 

Acesse AQUI o notebook no GitHub com o código completo. Por fim, não esqueça de mandar aquele feedback para nós e até a próxima.

Referências

• Confusion matrix and other metrics in machine learning
• Foundations of Imbalanced Learning
• An Introduction to Logistic Regression
• Explaining the Success of Nearest Neighbor Methods in Prediction

Conteúdos ao Cubo

Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.

• NLP com scikit-learn
• Processamento de Linguagem Natural com TensorFlow
• Modelos em Produção com Streamlit
• Deploy de Modelos com Heroku
• Agrupamento com scikit-learn
• Variáveis em Python
• Extrair Dados da API do Cartola FC
• Web Scraping e Coleta de Dados Automatizada com Python

Finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades. 

Tiago Dias

Apaixonado por dados e tecnologia ❤️ , criando soluções com dados 📊 📈 , desde 2015, sempre buscando tornar os processos orientados! Com formação em Engenharia da Computação 💾 , MBA Gestão da Informação e Business Intelligence e Especialização em Data Science.

Também atuo como professor na área de dados. Nas horas vagas crio modelos de Machine Learning 🤖 com Python em desafios do Kaggle e escrevo no Dados ao Cubo sobre o mundo dos dados 🎲 !

Compartilhando conhecimentos sempre 🚀