Data Science Machine Learning Python

Agrupamento com scikit-learn

On 10 de agosto de 2020, by Tiago Dias

Fala galera do mundo dos dados, partiu agrupamento com scikit-learn! Antes de mais nada, espero que estejam todos bem! Vamos para mais um post da nossa trilha de modelos de Machine Learning (ML) com sklearn. O nosso assunto de hoje é o agrupamento de dados, ou em outras palavras clusterização de dados. Agrupamento? Clusterização? E isso é modelo de machine learning? Vou te responder todas essas perguntas. 

Vamos ver um modelo de agrupamento bem popular, o k-means. Além disso, vamos ver também algumas formas de como avaliar o nosso modelo. Por fim, vamos comparar o nosso modelo com a classificação original dos dados. Sem mais enrolação, vamos entender o que é o agrupamento de dados. Partiu agrupamento com skearn!!!

Agrupamento de Dados

O modelo de agrupamento ou clusterização, nada mais que a divisão dos dados em grupos, que pode ser definido também como clusters. Essa separação dos dados se dá devido às características dos mesmos, ou seja, dados com características semelhantes tendem a ficar juntos. Mas isso é assim em um passe de mágica? Não né!

Vejamos um exemplo gráfico abaixo para fixar o entendimento do conceito. Temos a esquerda os dados apenas com duas variáveis x e y, e a direita os dados agrupados pelas semelhanças das suas variáveis.

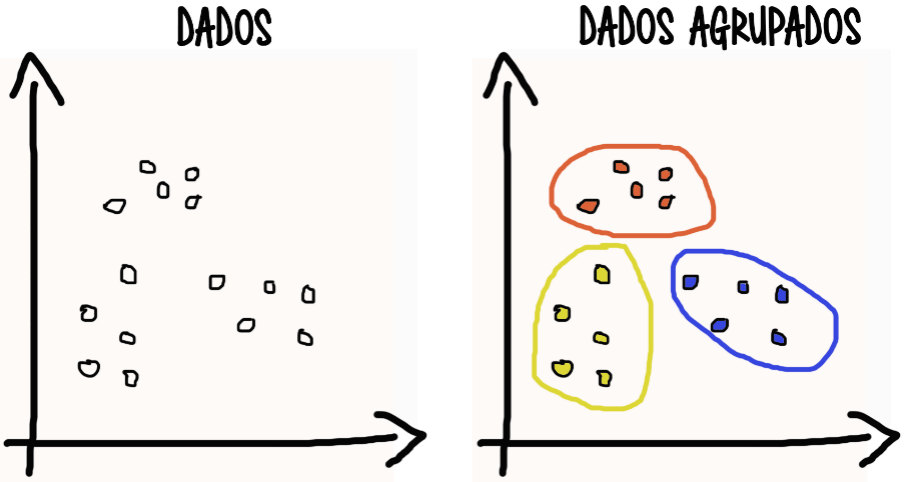
Agora que já temos esse conceito inicial vamos ser apresentados alguns modelos de machine learning para agrupamento de dados.

Modelos de Agrupamento de Dados

Existem diversos modelos de agrupamento na nossa conhecida biblioteca scikit-learn. O algoritmo linear k-médias (k-means) que separa em k grupos (pré-definidos) e agrupa os dados de acordo com as médias em relação a esses grupos. O DBSCAN é um algoritmo que separa os grupos de forma arbitrária de acordo com a densidade da amostra, identificando os pontos com mais densidade e criando grupos a partir desses pontos. O algoritmo de misturas gaussianas é não linear e probabilístico, similar ao k-means levando em consideração a distância entre os pontos, porém ele fornece as probabilidades de cada dado pertencer aos possíveis clusters.

Tiago só existe esse três modelos? Não, tem muito outros! Só tem os modelos da biblioteca scikit-learn? Também não. Aqui é o ponto de partida e o céu é o limite. E quais problemas os modelos de agrupamento resolvem? Ótima pergunta, se não resolver problemas não serve para quase nada. Então, vamos resolver problemas do tipo de aprendizagem não supervisionada, onde os dados não precisam possuir rótulos para serem agrupados. Temos os dados de entradas, e queremos descobrir similaridades, tirar insights desses dados. Por exemplo agrupar os clientes, dada algumas variáveis, como sexo, idade, região e renda (podem haver muitas outras, vai depender do problema) para descobrir os meus melhores clientes, ou agrupar em níveis de clientes (ouro, prata e bronze).

Vamos agora entender alguns tipos de agrupamentos existentes, para auxiliar no entendimento e resolução de problemas.

Tipos de Agrupamentos

Os agrupamentos de dados podem ser de diversos tipos, mas vamos abordar aqui 3 tipos mais comuns: os grupos exclusivos, sobrepostos e hierárquicos.

Grupos Exclusivos

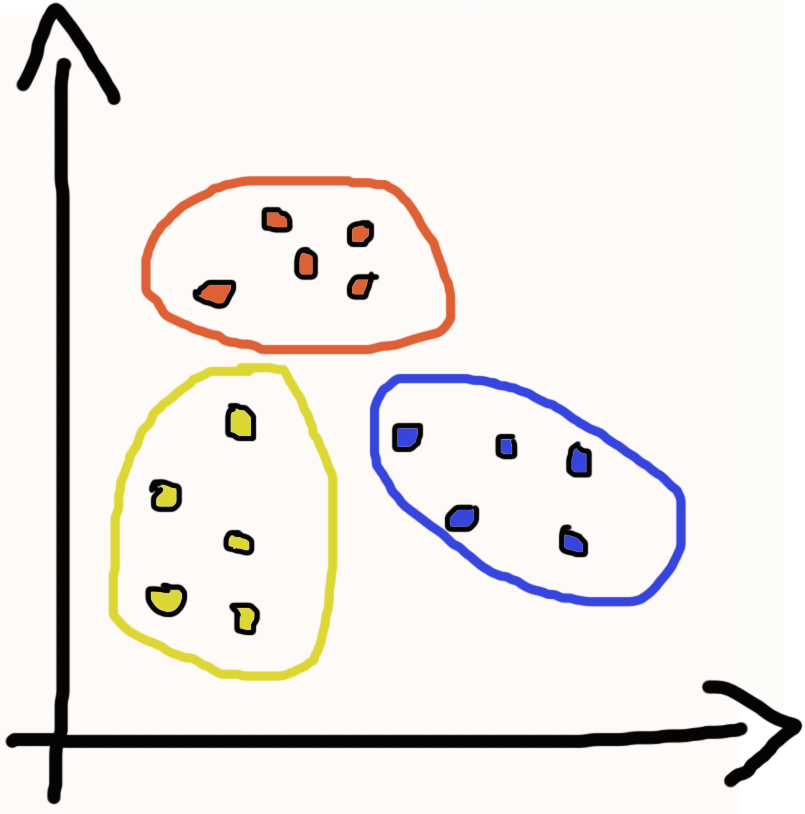
Os grupos exclusivos são quando cada observação pertence apenas a 1 grupo, de forma exclusivas dos demais, como o próprio nome sugere. Por exemplo, se temos um grupo de pessoas e queremos criar grupos a partir das idades dessas pessoas. Dessa forma cada pessoa pode ter apenas uma idade, então só pode pertencer a 1 grupo apenas. Se fomos representar de uma forma gráfica os grupos exclusivos, ficaria algo semelhante a imagem ao lado.

Grupos Sobrepostos

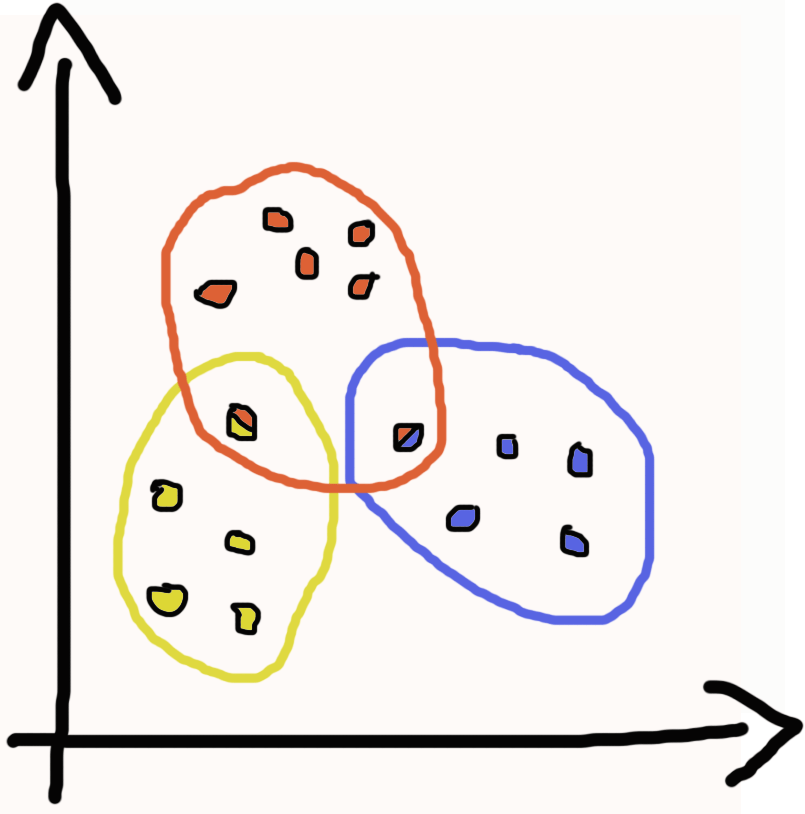
Já os grupos sobrepostos cada observação pode pertencer a 1 ou mais grupos, deixando os grupos sobrepostos. Por exemplo, se temos um grupo de pessoas e queremos criar grupos a partir dos idiomas falados por estas pessoas. Dessa forma cada pessoa pode pertencer a mais de um grupo, basta ela falar mais de 1 idioma, essas pessoas ficariam nas sobreposições dos grupos. Se fomos representar de uma forma gráfica os grupos sobrepostos, ficaria algo semelhante a imagem ao lado.

Grupos Hierárquicos

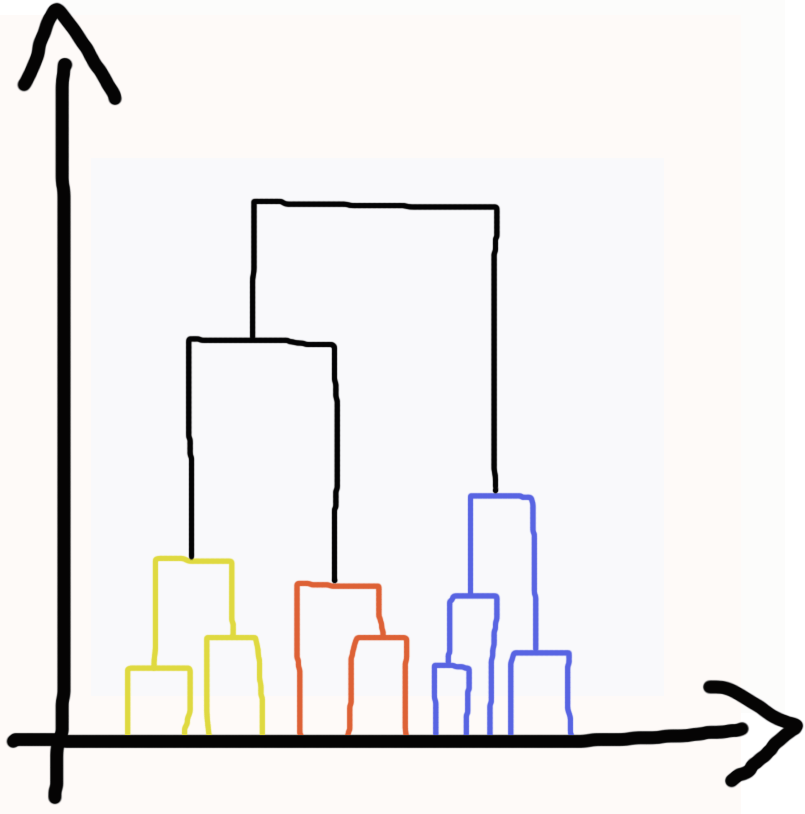
Por fim os grupos hierárquicos onde cada observação tem uma relação hierárquica entres os dados, montando uma hierarquia entre os atributos. Por exemplo, se temos um grupo de pessoas classificadas em crianças, adulto e idosos, então, temos três grupos de pessoas, e se abaixo temos os grupos com as idades dessas pessoas. Dessa forma temos uma relação hierárquica dos grupos de idade de 0 a 17 anos, onde todos esses grupos pertencem ao grupo crianças, e assim segue a mesma lógica para as outras idades que vão pertencer aos grupos adulto e idosos. Se fomos representar de uma forma gráfica os grupos hierárquicos, ficaria algo semelhante a imagem ao lado.

Agora que já sabemos o que é os agrupamentos de dados e os tipos mais comuns, vamos entender o algoritmo k-means da biblioteca scikit-learn, que cria modelos de machine learning do tipo agrupamento.

Modelo de Agrupamento K-means

Falando de maneira bem simples, o método de agrupamento k-means, separa os dados k grupos (onde o número de k é definido pelo cientista de dados) e as observações vão se agrupar ao k mais próximo da sua distância média.

Cada k tem um ponto denominado de centróide, que por sua vez é definido sempre a fim de minimizar a soma das distâncias quadradas das observações dos dados. Em outras palavras, o algoritmo mede a distância de cada observação para posicionar os centróides onde tiver a menor distância entre os pontos.

A escolha do número de k é realizada pelo cientista de dados, como informei anteriormente, mas existem algumas avaliações para auxiliar nessa decisão. Porém sabemos que esta é uma decisão também de negócio, portanto não existe certo ou errado. O que vai acontecer é uma divisão de grupos mais ou menos bem definidos. 

Agora vamos ver essa teoria na prática, vamos utilizar um dataset já conhecido nosso de outros posts, o iris. Assim, vamos aplicar o agrupamento nesses dados, fazer uma avaliação desses grupos gerados e por fim, fazer um comparativo com a classificação original dos dados. Abaixo vamos ver um passo a passo em python para aplicar o kmeans e realizar a clusterização.

Importar bibliotecas

import seaborn as sns
import pandas as pd
from sklearn.cluster import KMeans

Selecionar dataset

# Selecionando os dados do iris
df = sns.load_dataset("iris")

Verificar dados

# Nome das espécies de flores
list(df['species'].unique())

Selecionar variáveis de entrada

X = df.drop(columns='species').copy()

K-means com sklearn

kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)

# Centroides das entradas
kmeans.cluster_centers_

# Clusters das entradas
kmeans.labels_

Agora que já temos os dados carregados, podemos fazer uma avaliação do modelo de machine learning. Importante para uma análise da qualidade da divisão dos grupos.

Avaliação do Modelo de Agrupamento

Vamos ver agora os métodos Elbow, também conhecido como método do cotovelo e o método Silhouette para avaliar se o nosso modelo de agrupamento está com uma boa performance.

Método Elbow

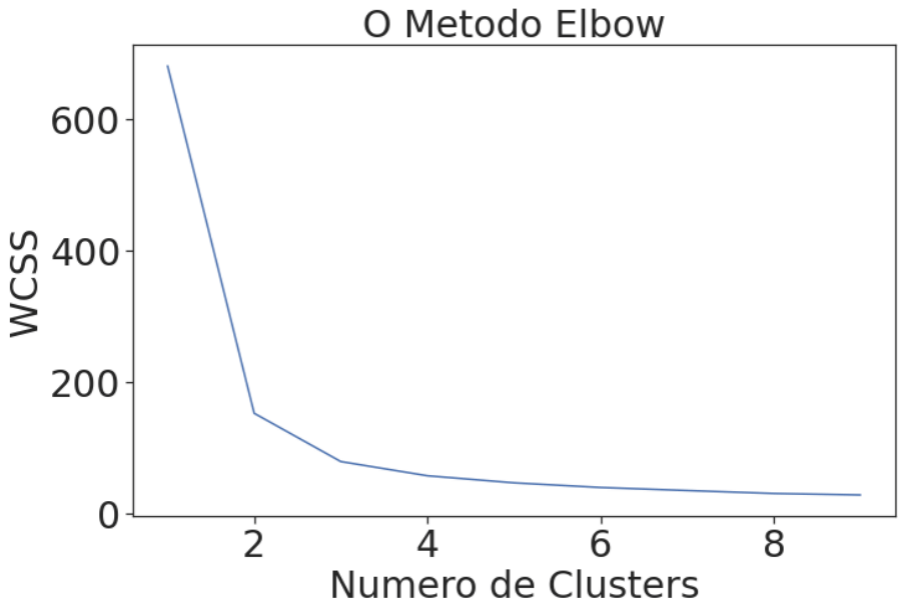
O método visa auxiliar na escolha da quantidade de grupos, ou seja, do valor de k. Gerando uma curva similar a um cotovelo (tradução do nome do método), ajuda a identificar o número de grupos, mostrando até que ponto com o aumento do número de k não existe ganho. No gráfico abaixo podemos definir esse número de clusters em 3.

Método Silhouette 

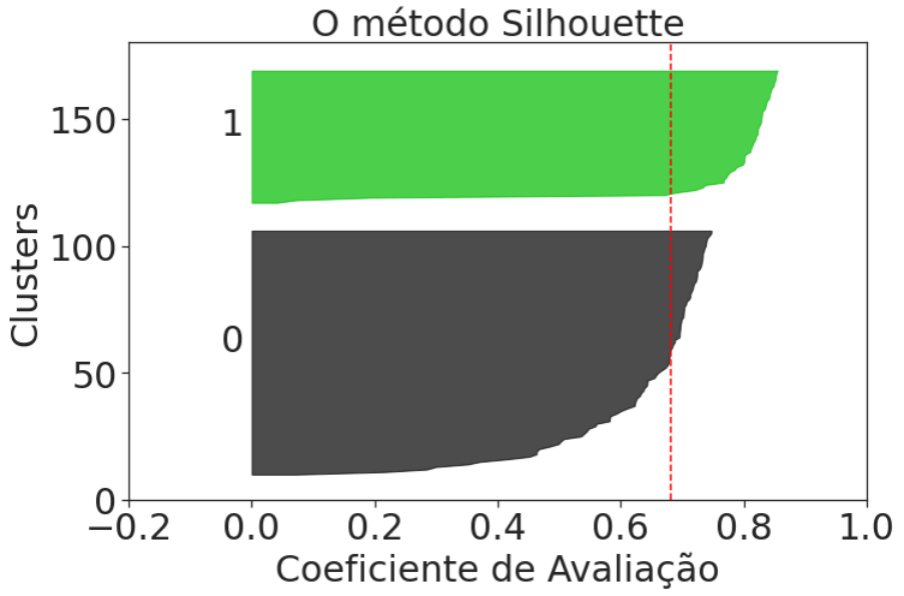
Um outra análise para avaliar o resultado dos clusters gerados uma das métricas é a silhouette_score, onde o melhor valor é 1 e o pior valor é -1. Valores próximos a 0 indicam clusters sobrepostos. Valores negativos geralmente indicam que uma amostra foi atribuída ao cluster errado. Podemos visualizar no gráfico abaixo, onde a linha tracejada vermelha representa o silhouette_score, e está próximo a 0,7 para 2 clusters sendo a melhor divisão segundo o critério do Silhouette.

Cluster x Classificação do Dados

Por último, uma validação da divisão dos clusters comparado com a classificação original dos dados. Essa avaliação só foi possível devido os rótulos dos dados serem conhecidos, o que não ocorre na maioria dos problemas de agrupamento. Vejamos o código python abaixo que identifica o cluster que tem a maior quantidade de uma classe e verifica quantos acertos houve naquele cluster.

# Validação da divisão dos clusters
X_valida = X.copy()
df_valida = df.copy()
for i in range(2, 6):
    kmeans_valida = KMeans(n_clusters = i)
    kmeans_valida.fit(X_valida)
    df_valida['kmeans'] = kmeans_valida.labels_
    print('K =', i)
    for j in list(df['species'].unique()):
        per_valida = df_valida.query('species == @j')['kmeans'].value_counts().max()/df_valida.query('species == @j').shape[0]
        class_valida = df_valida.query('species == @j')['kmeans'].value_counts().index[0]
        print('Espécie {}'.format(j), 'Cluster', class_valida, '- Percentual de acerto {:.0%}'.format(per_valida))
    print(55*'=')

K = 2
Espécie setosa Cluster 1 - Percentual de acerto 100%
Espécie versicolor Cluster 0 - Percentual de acerto 94%
Espécie virginica Cluster 0 - Percentual de acerto 100%
=======================================================
K = 3
Espécie setosa Cluster 1 - Percentual de acerto 100%
Espécie versicolor Cluster 0 - Percentual de acerto 96%
Espécie virginica Cluster 2 - Percentual de acerto 72%
=======================================================
K = 4
Espécie setosa Cluster 1 - Percentual de acerto 100%
Espécie versicolor Cluster 0 - Percentual de acerto 54%
Espécie virginica Cluster 2 - Percentual de acerto 64%
=======================================================
K = 5
Espécie setosa Cluster 0 - Percentual de acerto 100%
Espécie versicolor Cluster 1 - Percentual de acerto 52%
Espécie virginica Cluster 2 - Percentual de acerto 48%
=======================================================

Analisando os resultados, em números a divisão de clusters ideal seria 2 (confere com a análise do Método Silhouette), mas como os dados são conhecidos e sabemos que existe 3 espécies nele presente, logo o melhor número de clusters é 3 (confere com a análise do Método Elbow). A escolha desse exemplo foi justamente para mostrar a importância de conhecermos os nossos dados e o negócio por trás daqueles dados, e como os números podem nos enganar ou nos alertar! A análise dos resultados é tão importante quanto a criação de um modelo.

Agrupamento com scikit-learn ao Cubo

Enfim! Aqui temos uma introdução ao cluster de dados, onde praticamos o agrupamento com scikit-learn, e vimos quais os problemas que esses modelos de machine learning se propõe a resolver. Além disso vimos algumas formas de avaliar nossos modelos de clusterização. 

Isso é o que tem para hoje! Espero que curtam o conteúdo, não deixa de mandar aquele feedback. Se quiser ver algum assunto que não abordamos ainda, envia uma mensagem para nós. Se quiser você mesmo escrever sobre algum tema relacionado a ciência de dados venha ser NOSSO PARCEIRO!

E não deixe de conferir o NOTEBOOK que tem todo esse código e mais algumas dicas legais. Até a próxima!

Referências

Conteúdos ao Cubo

Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.

Finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades. 

Gostou? Compartilhe!

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *