Inteligência Artificial em Ressonância Magnética

On 15 de agosto de 2020, by Rodrigo Oliveira

Ok, vamos melhorar um pouco mais o título desse post:

Auto-Segmentação de Tumor Cerebral em Imagens de Ressonância Magnética (MRI) usando Inteligência Artificial!!!

What!? Está me dizendo que irá usar Redes Neurais Artificiais, que tentam simular o cérebro humano, justamente para estudá-lo?

Muita calma nessa hora… vamos deixar para usar o cérebro daqui a pouco! Aliás, vamos fatiá-lo um pouquinho!

O que irão ver neste post é como construir uma rede neural artificial para segmentar automaticamente as regiões de um tumor no cérebro, usando os exames de ressonância magnética. Agora ficou mais simples, não?!!!

Eu sei que não é nada fácil mas vamos tentar simplificar (se isso é possível) e mostrar um passo a passo de como fazer isso usando o bom e velho Python (e mais uns pacotes adicionais).

As etapas que irei apresentar são:

O que é uma Imagem de Ressonância Magnética
Explorando o conjunto de dados
Definindo a Arquitetura da Rede Neural Artificial
Métricas e Funções de Perda para Segmentação
Criando e Treinando o Modelo
Visualizar e Avaliar as Previsões

1. O que é um MRI

Magnetic Resonance Imaging (MRI) é uma técnica de imagem médica avançada usada em Radiologia para formar imagens da anatomia e dos processos fisiológicos do corpo. Em um alto nível, a ressonância magnética funciona medindo as ondas de rádio emitidas por átomos submetidos a um campo magnético.

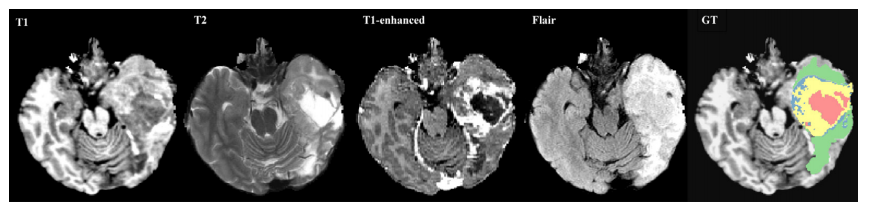
Inteligência Artificial em ressonância magnética

Vamos construir um modelo de segmentação multiclasse, identificando três anormalidades diferentes em cada imagem: Edemas, Tumores sem Realce e Tumores com Realce

2. Explorando os dados do MRI

Frequentemente encontramos imagens de ressonância magnética no formato DICOM. É um formato de saída da maioria dos scanners comerciais. Este tipo de dado pode ser processado usando a biblioteca pydicom do Python.

Para executar esta tarefa precisamos de dados, muitos dados. E nesse caso, muitas imagens do cérebro!

Então vamos utilizar os dados do Decathlon 10 Challenge, onde tem um repositório com essas imagens, em sua maioria, pré-processados para os participantes da competição. Mas, na prática, os dados de ressonância magnética precisam ser significativamente pré-processados antes de usá-los para treinar os modelos.

O nosso conjunto de dados está armazenado no formato NIfTI-1 e usaremos a biblioteca NiBabel para manipular os arquivos. Cada amostra de treinamento é composta por dois arquivos separados:

O primeiro é um arquivo de imagens contendo um array 4D no formato (240x240x155x4);
O segundo é um arquivo de etiqueta (labels) contendo uma matriz 3D no formato (240x240x155);

Os rótulos dessa matriz do segundo arquivo estão classificados da seguinte forma:

0: background
1: edema
2: tumor sem realce
3: tumor com realce

Temos acesso a um total de 484 imagens, onde iremos dividir em 80% para treinamento e 20% para validação.

Let’s code!!! Vamos começar examinando um único caso e visualizando os dados!

DATA_DIR = '../data/'
def load_case(image_nifty_file, label_nifty_file):
    # carregar a imagem e o arquivo de rotulos
    # obter o conteúdo da imagem
    # retornar um array numpy
    image = np.array(nib.load(image_nifty_file).get_fdata())
    label = np.array(nib.load(label_nifty_file).get_fdata())
    
    return image, label
    
image, label = load_case(DATA_DIR + "imagesTr/BRATS_003.nii.gz", DATA_DIR + "labelsTr/BRATS_003.nii.gz")
image = util.get_labeled_image(image, label)

util.plot_image_grid(image)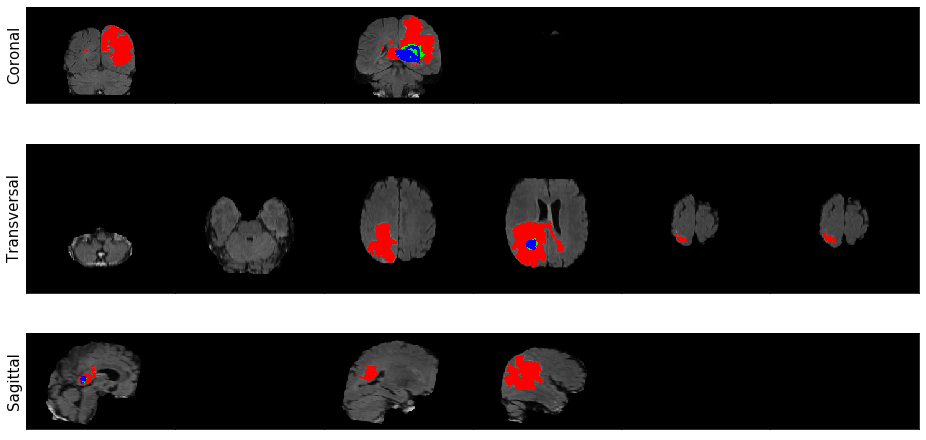

As cores correspondem a cada uma das classes:

Vermelho é Edema;
Verde é um Tumor sem Realce;
Azul é um Tumor com Realce;

É possível também utilizar a função para gerar um gif que mostra a iteração em cada eixo:

image, label = load_case(DATA_DIR + "imagesTr/BRATS_003.nii.gz", DATA_DIR + "labelsTr/BRATS_003.nii.gz")
util.visualize_data_gif(util.get_labeled_image(image, label))

2.1. Pré-processamento dos dados

Como assim, pré-processar os dados? Você disse que os dados da competição já estão prontinhos?

Eu sei, eu sei… Por mais que no nosso conjunto de dados já está pré-processado e no formato NIfTI, precisamos fazer pequenos ajustes antes de alimentar a nossa rede neural!

Primeiro, vamos gerar “patches”de nossos dados (pode considerar como sendo sub-volumes de todas as MRIs).

A razão pela qual estamos gerando “patches” é porque simplesmente não caberá todo o volume de dados na memória da GPU 😉
Além disso, dado que uma grande parte dos volumes de ressonância magnética são apenas tecido cerebral ou fundo preto sem quaisquer tumores, queremos ter certeza de que escolhemos partes que incluem pelo menos alguma quantidade de dados do tumor;

def get_sub_volume(image, label, 
                   orig_x = 240, orig_y = 240, orig_z = 155, 
                   output_x = 160, output_y = 160, output_z = 16,
                   num_classes = 4, max_tries = 1000, background_threshold=0.95):

    # Initialize features and labels with `None`
    X = None
    y = None
    tries = 0
    
    while tries < max_tries:
        # randomly sample sub-volume by sampling the corner voxel
        # hint: make sure to leave enough room for the output dimensions!
        start_x = np.random.randint(0, orig_x - output_x+1)
        start_y = np.random.randint(0, orig_y - output_y+1)
        start_z = np.random.randint(0, orig_z - output_z+1)

        # extract relevant area of label
        y = label[start_x: start_x + output_x,
                  start_y: start_y + output_y,
                  start_z: start_z + output_z]
        
        # One-hot encode the categories.
        # This adds a 4th dimension, 'num_classes'
        # (output_x, output_y, output_z, num_classes)
        y = keras.utils.to_categorical(y, num_classes=num_classes)

        # compute the background ratio
        bgrd_ratio = np.sum(y[:, :, :, 0])/(output_x * output_y * output_z)

        # increment tries counter
        tries += 1

        # if background ratio is below the desired threshold,
        # use that sub-volume.
        # otherwise continue the loop and try another random sub-volume
        if bgrd_ratio < background_threshold:

            # make copy of the sub-volume
            X = np.copy(image[start_x: start_x + output_x,
                              start_y: start_y + output_y,
                              start_z: start_z + output_z, :])
            
            # change dimension of X
            # from (x_dim, y_dim, z_dim, num_channels)
            # to (num_channels, x_dim, y_dim, z_dim)
            X = np.moveaxis(X, 3, 0)

            # change dimension of y
            # from (x_dim, y_dim, z_dim, num_classes)
            # to (num_classes, x_dim, y_dim, z_dim)
            y = np.moveaxis(y, 3, 0)

            # take a subset of y that excludes the background class
            # in the 'num_classes' dimension
            y = y[1:, :, :, :]
    
            return X, y

    # if we've tried max_tries number of samples
    # Give up in order to avoid looping forever.
    print(f"Tried {tries} times to find a sub-volume. Giving up...")

E então, executando essa função, podemos examinar um “patch candidato” e garantir que está funcionando corretamente:

image, label = load_case(DATA_DIR + "imagesTr/BRATS_001.nii.gz", DATA_DIR + "labelsTr/BRATS_001.nii.gz")
X, y = get_sub_volume(image, label)

# enhancing tumor is channel 2 in the class label
# you can change indexer for y to look at different classes
util.visualize_patch(X[0, :, :, :], y[2])

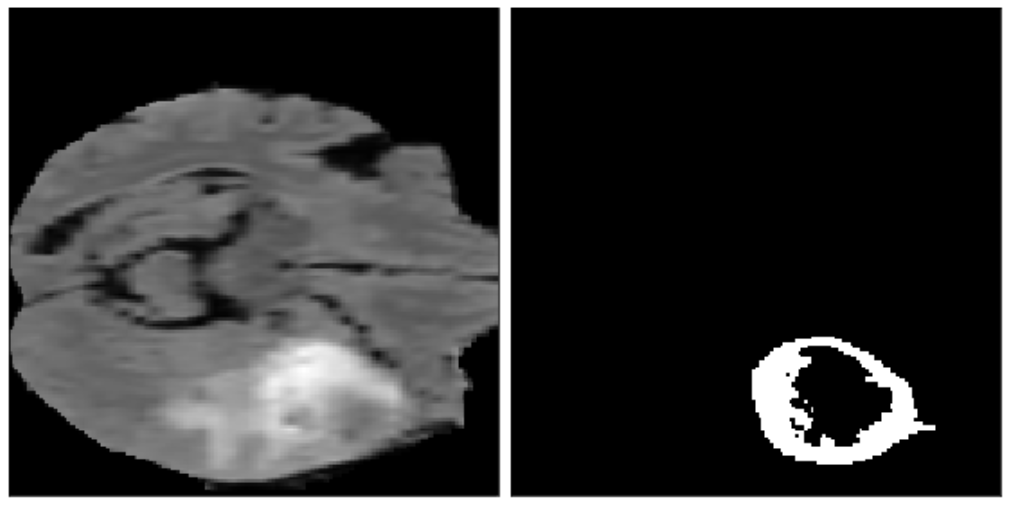
Segundo, vamos padronizar os dados (média 0 e desvio padrão 1). Essa é uma técnica comum no processamento de imagens profundas, pois a padronização torna muito mais fácil o aprendizado da rede neural artificial.

def standardize(image):

    # initialize to array of zeros, with same shape as the image
    standardized_image = np.zeros(image.shape)

    # iterate over channels
    for c in range(image.shape[0]):
        # iterate over the `z` dimension
        for z in range(image.shape[3]):
            # get a slice of the image 
            # at channel c and z-th dimension `z`
            image_slice = image[c,:,:,z]

            # subtract the mean from image_slice
            centered = image_slice - np.mean(image_slice)
            
            # divide by the standard deviation (only if it is different from zero)
            if np.std(centered) != 0:
                centered_scaled = centered / np.std(centered)

            # update  the slice of standardized image
            # with the scaled centered and scaled image
            standardized_image[c, :, :, z] = centered_scaled

    return standardized_image
    
    
X_norm = standardize(X)
print("standard deviation for a slice should be 1.0")
print(f"stddv for X_norm[0, :, :, 0]: {X_norm[0,:,:,0].std():.2f}")

Vamos visualizar novamente nosso “patch” apenas para ter certeza que não vai ser diferente (mesmo que a função imshow que usamos normaliza automaticamente os pixels quando exibidos em preto e branco):

util.visualize_patch(X_norm[0, :, :, :], y[2])

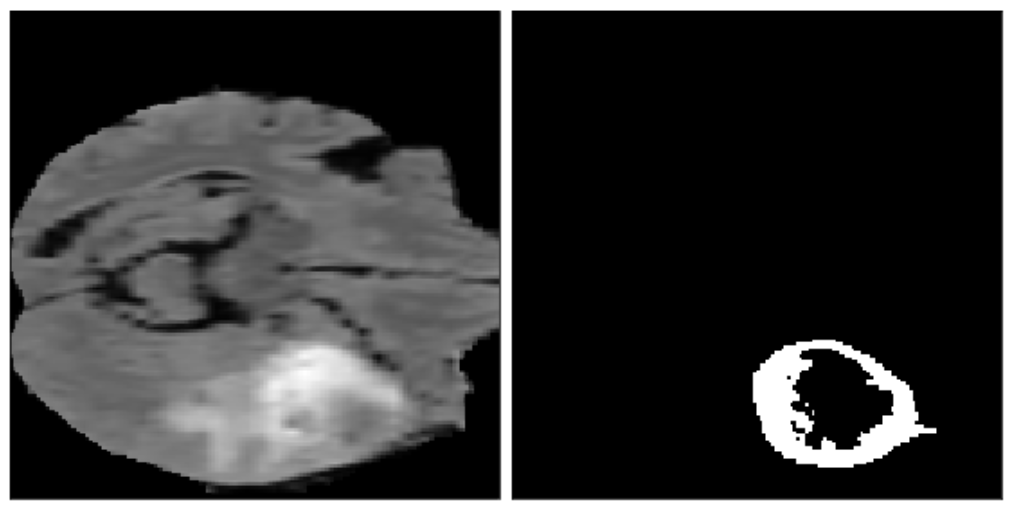
Tudo tranquilo até aqui? Porque a diversão ainda está por vir!

3. Definindo a Arquitetura da Rede Neural Artificial

Agora vamos definir nosso modelo. E o candidato escolhido para esta missão será o modelo 3D U-Net. Além de ser um dos modelos de melhor desempenho para a tarefa, possui uma arquitetura que aproveitará a forma volumétrica das imagens de ressonância magnética.

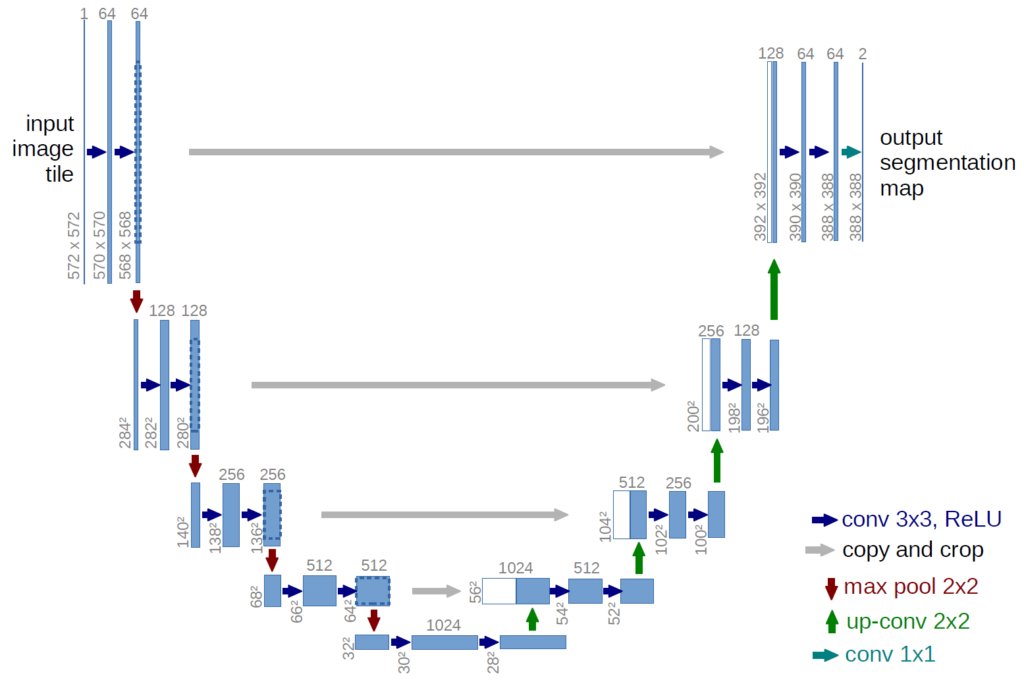
4. Métricas e Função de Perda

4.1. Coeficiente de Similaridade de Dados

Além da arquitetura, um dos elementos mais importantes de qualquer método de aprendizado profundo é a escolha da nossa função de perda. Uma escolha natural com a qual você pode estar familiarizado é a função de perda de entropia cruzada (cross-entropy).

No entanto, essa função de perda não é ideal para tarefas de segmentação devido ao grande desequilíbrio de classe (normalmente não há muitas regiões positivas). Uma perda muito mais comum para tarefas de segmentação é o coeficiente de similaridade de dados, que é uma medida de quão bem dois contornos se sobrepõem.

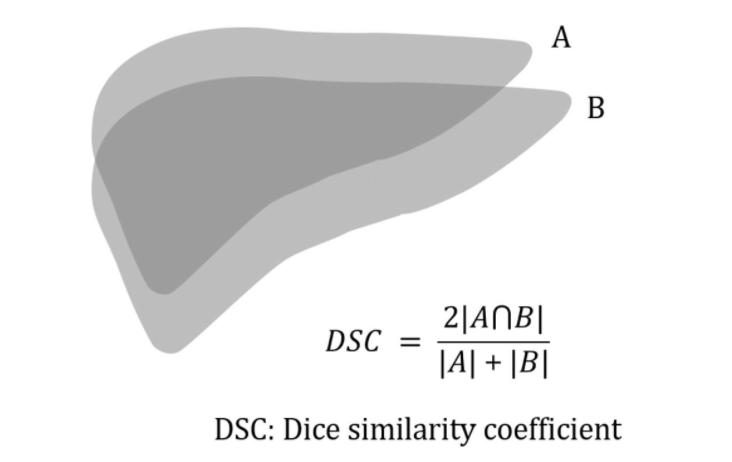
def single_class_dice_coefficient(y_true, y_pred, axis=(0, 1, 2), epsilon=0.00001):

    dice_numerator   = 2. * K.sum(y_true * y_pred, axis=axis) + epsilon
    dice_denominator = K.sum(y_true, axis=axis) + K.sum(y_pred, axis=axis) + epsilon
    dice_coefficient = (dice_numerator) / (dice_denominator)

    return dice_coefficient

4.2. Coeficiente de Similaridade de Dados para Várias Classes

Agora que temos uma função de perda para uma única classe, podemos pensar sobre como abordar para um contexto de várias classes, lembrando que, no nosso caso, queremos segmentações para cada uma das 3 classes de anormalidades: edema, tumor sem realce e tumor com realce.

Isso nos dará 3 coeficientes de dados diferentes, um para cada classe de anormalidade. Para combiná-los, podemos apenas calcular a média, usando K.mean():

def dice_coefficient(y_true, y_pred, axis=(1, 2, 3),epsilon=0.00001):

    dice_numerator   = 2. * K.sum(y_true * y_pred, axis=axis) + epsilon
    dice_denominator = K.sum(y_true, axis=axis) + K.sum(y_pred, axis=axis) + epsilon
    dice_coefficient = K.mean((dice_numerator)/(dice_denominator))

    return dice_coefficient

5. Criando e Treinando o Modelo 3D U-Net

Primeiro, vamos implementar a função unet_model_3d que criará a arquitetura do modelo e irá compilar as funções de perda e métricas especificadas.

def unet_model_3d(loss_function, input_shape=(4, 160, 160, 16),
                  pool_size=(2, 2, 2), n_labels=3,
                  initial_learning_rate=0.00001,
                  deconvolution=False, depth=4, n_base_filters=32,
                  include_label_wise_dice_coefficients=False, metrics=[],
                  batch_normalization=False, activation_name="sigmoid"):
  
    inputs = Input(input_shape)
    current_layer = inputs
    levels = list()

    # add levels with max pooling
    for layer_depth in range(depth):
        layer1 = create_convolution_block(input_layer=current_layer,
                                          n_filters=n_base_filters * (
                                                  2 ** layer_depth),
                                          batch_normalization=batch_normalization)
        layer2 = create_convolution_block(input_layer=layer1,
                                          n_filters=n_base_filters * (
                                                  2 ** layer_depth) * 2,
                                          batch_normalization=batch_normalization)
        if layer_depth < depth - 1:
            current_layer = MaxPooling3D(pool_size=pool_size)(layer2)
            levels.append([layer1, layer2, current_layer])
        else:
            current_layer = layer2
            levels.append([layer1, layer2])

    # add levels with up-convolution or up-sampling
    for layer_depth in range(depth - 2, -1, -1):
        up_convolution = get_up_convolution(pool_size=pool_size,
                                            deconvolution=deconvolution,
                                            n_filters=
                                            current_layer._keras_shape[1])(
            current_layer)
        concat = concatenate([up_convolution, levels[layer_depth][1]], axis=1)
        current_layer = create_convolution_block(
            n_filters=levels[layer_depth][1]._keras_shape[1],
            input_layer=concat, batch_normalization=batch_normalization)
        current_layer = create_convolution_block(
            n_filters=levels[layer_depth][1]._keras_shape[1],
            input_layer=current_layer,
            batch_normalization=batch_normalization)

    final_convolution = Conv3D(n_labels, (1, 1, 1))(current_layer)
    act = Activation(activation_name)(final_convolution)
    model = Model(inputs=inputs, outputs=act)

    if not isinstance(metrics, list):
        metrics = [metrics]

    model.compile(optimizer=Adam(lr=initial_learning_rate), loss=loss_function,
                  metrics=metrics)
    return model

E então, chamamos a função para criar nosso modelo 3D U-Net:

model = util.unet_model_3d(loss_function=soft_dice_loss, metrics=[dice_coefficient])

5.1. Treinamento do modelo usando um grande conjunto de dados

Para facilitar o treinamento do modelo em um grande conjunto de dados podemos usar a técnica de “patches” e armazená-los no formato “hdf5“.

base_dir = DATA_DIR + "processed/"

with open(base_dir + "config.json") as json_file:
    config = json.load(json_file)

# Get generators for training and validation sets
train_generator = util.VolumeDataGenerator(config["train"], base_dir + "train/", batch_size=3, dim=(160, 160, 16), verbose=0)
valid_generator = util.VolumeDataGenerator(config["valid"], base_dir + "valid/", batch_size=3, dim=(160, 160, 16), verbose=0)

steps_per_epoch  = 20
n_epochs         = 10
validation_steps = 20

model.fit_generator(generator=train_generator,
                    steps_per_epoch=steps_per_epoch,
                    epochs=n_epochs,
                    use_multiprocessing=True,
                    validation_data=valid_generator,
                    validation_steps=validation_steps)

model.save_weights(base_dir + 'my_model_pretrained.hdf5')

Travou o computador depois de algumas horas processando??!

OK, ok, te entendo… precisamos de um alto poder computacional e uma GPU.

Então vamos simplificar um pouco!

5.2. Carregando um modelo pré-treinado

Não disse que iria facilitar sua vida?! Vamos importar uma versão modelo pré-treinado.

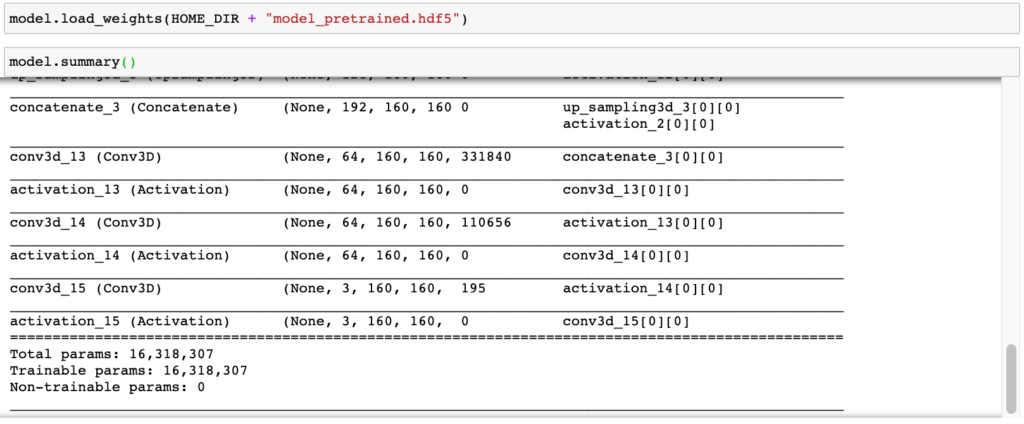
16.318.307 parametros tem a nossa rede neural artificial. É muita coisa!!!!

6. Visualizar e Avaliar as Previsões

Agora que temos um modelo treinado, vamos aprender a extrair suas previsões e avaliar o seu desempenho no conjunto de dados de validação.

6.1. Desempenho do Modelo

Primeiro, vamos medir o desempenho geral no conjunto de validação. Podemos fazer isso chamando a função “evaluate_generator” do Keras.

val_loss, val_dice = model.evaluate_generator(valid_generator)

print(f"validation soft dice loss: {val_loss:.4f}")
print(f"validation dice coefficient: {val_dice:.4f}")

Uma observação: aqui estamos usando 20% dos dados para validação, porém, na vida real, o ideal é utilizar a validação cruzada (cross-validation), escolher os melhores hyperparâmetros e, em seguida, utilizar o conjunto de testes para avaliar o modelo.

6.2. Previsões no nível de patches

Podemos obter as previsões chamando a função “predict” do nosso modelo.

X_norm_with_batch_dimension = np.expand_dims(X_norm, axis=0)
patch_pred = model.predict(X_norm_with_batch_dimension)

Será necessário converter a previsões de probabilidades em uma categoria. Atualmente, cada elemento dentro de “patch_pred” é um número entre 0 e 1.

Cada número é a confiança do modelo de que um “voxel” faz parde de uma determinada classe.

Vamos converter em inteiros discretos de 0 e 1 usando um limite de 0.5 (em aplicações reais é possível ajustar esse limite para atingir o nível necessário de sensibilidade ou especificidade).

# set threshold.
threshold = 0.5

# use threshold to get hard predictions
patch_pred[patch_pred > threshold] = 1.0
patch_pred[patch_pred <= threshold] = 0.0

Agora vamos visualizar o patch original e nossas previsões:

print("Patch and ground truth")
util.visualize_patch(X_norm[0, :, :, :], y[2])
plt.show()
print("Patch and prediction")
util.visualize_patch(X_norm[0, :, :, :], patch_pred[0, 2, :, :, :])
plt.show()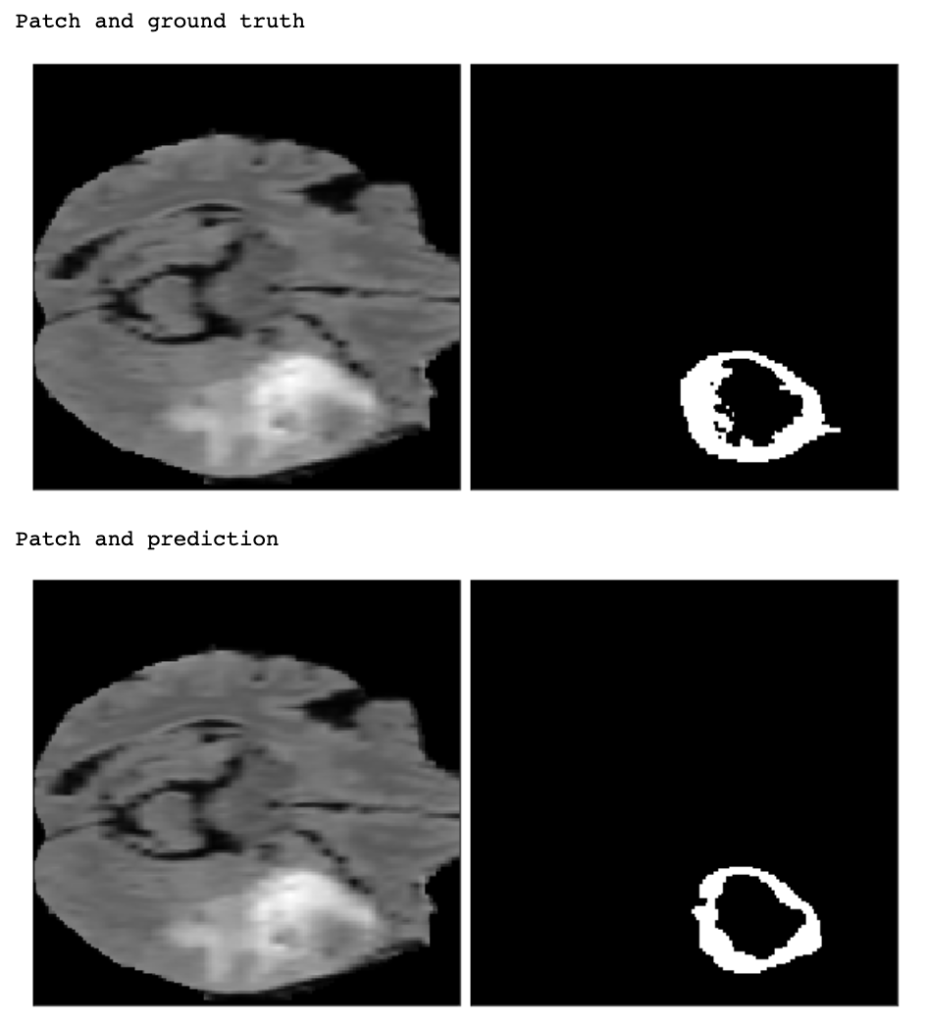

6.3. Sensibilidade e Especificidade

O modelo cobre algumas áreas relevantes, mas não é perfeito. Então para quantificar seu desempenho, podemos usar a sensibilidade e especificidade por pixel.

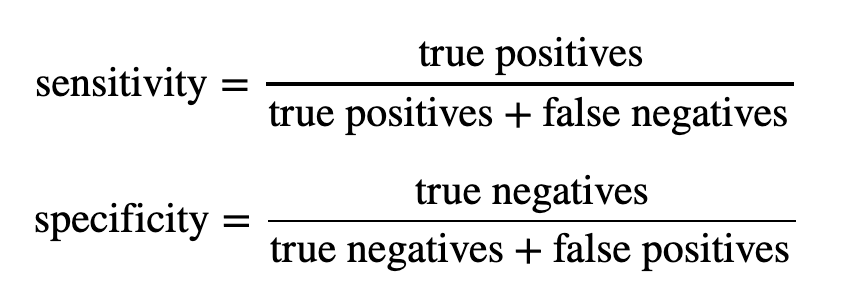
Vamos criar uma função para calcular a sensibilidade e especificidade:

def compute_class_sens_spec(pred, label, class_num):

    # extract sub-array for specified class
    class_pred = pred[class_num]
    class_label = label[class_num]

    # true positives
    tp = np.sum((class_pred == 1) & (class_label == 1))

    # true negatives
    tn = np.sum((class_pred == 0) & (class_label == 1))
    
    #false positives
    fp = np.sum((class_pred == 1) & (class_label == 0))
    
    # false negatives
    fn = np.sum((class_pred == 0) & (class_label == 0))

    # compute sensitivity and specificity
    sensitivity = tp / (tp + fn)
    specificity = tn / (tn + fp)

    return sensitivity, specificity

E também para visualizar essas métricas para cada classe

def get_sens_spec_df(pred, label):
    patch_metrics = pd.DataFrame(
        columns = ['Edema', 
                   'Non-Enhancing Tumor', 
                   'Enhancing Tumor'], 
        index = ['Sensitivity',
                 'Specificity'])
    
    for i, class_name in enumerate(patch_metrics.columns):
        sens, spec = compute_class_sens_spec(pred, label, i)
        patch_metrics.loc['Sensitivity', class_name] = round(sens,4)
        patch_metrics.loc['Specificity', class_name] = round(spec,4)

    return patch_metrics

6.4. Processando para todos os scans

Até aqui, nosso modelo funcionou apenas em “patches”, mas o que realmente queremos ver é o resultado do nosso modelo em todos os scans de ressonância magnética.

Então, vamos criar uma função para realizar as previsões e visualizações:

def predict_and_viz(image, label, model, threshold, loc=(100, 100, 50)):
    image_labeled = get_labeled_image(image.copy(), label.copy())

    model_label = np.zeros([3, 320, 320, 160])

    for x in range(0, image.shape[0], 160):
        for y in range(0, image.shape[1], 160):
            for z in range(0, image.shape[2], 16):
                patch = np.zeros([4, 160, 160, 16])
                p = np.moveaxis(image[x: x + 160, y: y + 160, z:z + 16], 3, 0)
                patch[:, 0:p.shape[1], 0:p.shape[2], 0:p.shape[3]] = p
                pred = model.predict(np.expand_dims(patch, 0))
                model_label[:, x:x + p.shape[1],
                y:y + p.shape[2],
                z: z + p.shape[3]] += pred[0][:, :p.shape[1], :p.shape[2],
                                      :p.shape[3]]

    model_label = np.moveaxis(model_label[:, 0:240, 0:240, 0:155], 0, 3)
    model_label_reformatted = np.zeros((240, 240, 155, 4))

    model_label_reformatted = to_categorical(label, num_classes=4).astype(
        np.uint8)

    model_label_reformatted[:, :, :, 1:4] = model_label

    model_labeled_image = get_labeled_image(image, model_label_reformatted,
                                            is_categorical=True)

    fig, ax = plt.subplots(2, 3, figsize=[10, 7])

    # plane values
    x, y, z = loc

    ax[0][0].imshow(np.rot90(image_labeled[x, :, :, :]))
    ax[0][0].set_ylabel('Ground Truth', fontsize=15)
    ax[0][0].set_xlabel('Sagital', fontsize=15)

    ax[0][1].imshow(np.rot90(image_labeled[:, y, :, :]))
    ax[0][1].set_xlabel('Coronal', fontsize=15)

    ax[0][2].imshow(np.squeeze(image_labeled[:, :, z, :]))
    ax[0][2].set_xlabel('Transversal', fontsize=15)

    ax[1][0].imshow(np.rot90(model_labeled_image[x, :, :, :]))
    ax[1][0].set_ylabel('Prediction', fontsize=15)

    ax[1][1].imshow(np.rot90(model_labeled_image[:, y, :, :]))
    ax[1][2].imshow(model_labeled_image[:, :, z, :])

    fig.subplots_adjust(wspace=0, hspace=.12)

    for i in range(2):
        for j in range(3):
            ax[i][j].set_xticks([])
            ax[i][j].set_yticks([])

    return model_label_reformatted

Executando esse código, podemos ver o resultado:

image, label = load_case(DATA_DIR + "imagesTr/BRATS_003.nii.gz", DATA_DIR + "labelsTr/BRATS_003.nii.gz")
pred = util.predict_and_viz(image, label, model, .5, loc=(130, 130, 77))

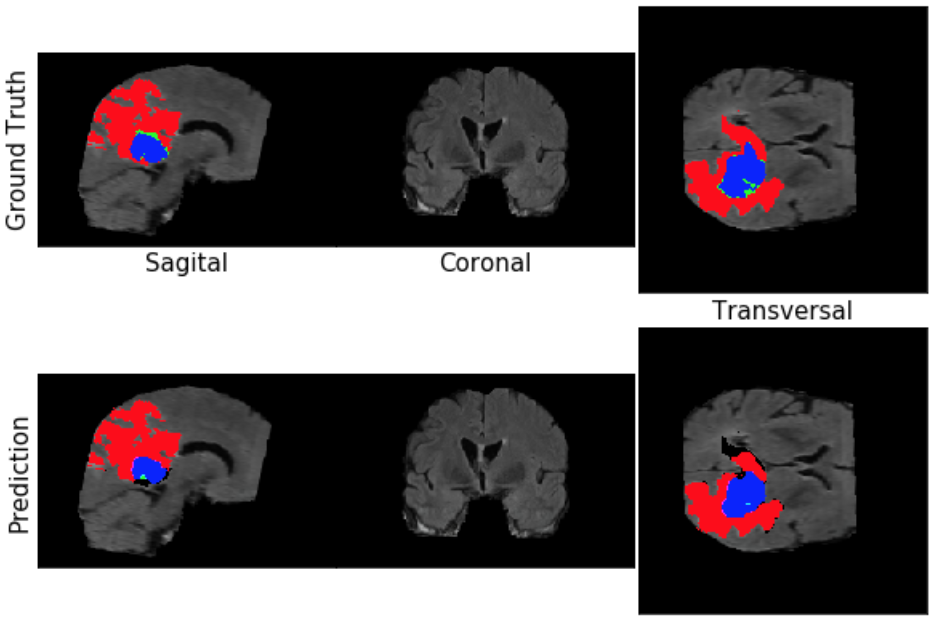
Podemos verificar que tiveram algumas diferenças entre o original e as previsões. Vamos usar a função de sensibilidade e especificidade que criamos anteriores para avaliar o desempenho.

whole_scan_label = keras.utils.to_categorical(label, num_classes = 4)
whole_scan_pred = pred

# move axis to match shape expected in functions
whole_scan_label = np.moveaxis(whole_scan_label, 3 ,0)[1:4]
whole_scan_pred = np.moveaxis(whole_scan_pred, 3, 0)[1:4]

whole_scan_df = get_sens_spec_df(whole_scan_pred, whole_scan_label)

É isso então pessoal. Espero que tenham gostado.

Sei que não é uma tarefa fácil, mas estamos vendo cada vez mais o uso de Inteligência Artificial ajudando a área da Saúde e Medicina.

O projeto complete pode ser acessado neste link: IA_Magnetic_Resonance_Imaging

Links úteis:

Conteúdos ao Cubo

Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.

Finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades.

Rodrigo Oliveira

Cientista de Dados na Unimed Blumenau. Apaixonado por tecnologia, atualmente tem se dedicado a projetos voltados para a aplicação da Ciência de Dados e Inteligência Artificial na área de Saúde e Medicina.

Gostou? Compartilhe!