Fala, galera! Tudo bem? Tudo certinho aí? Esse é o primeiro post da trilha de Pré-processamento de dados, iremos falar de Feature Engineering (Engenharia de Atributos, em tradução livre). Mas em que consiste a engenharia de atributos? Ela consiste em pré-processar os dados para que fiquem da maneira adequada para serem utilizados por um modelo de machine learning. Como? Imputando valores a dados faltantes ou eliminando as observações com dados faltantes, removendo outliers (valores discrepantes), normalizando e padronizando variáveis numéricas, convertendo dados categóricos em numéricos, criando e extraindo novos atributos. Nesse post iremos abordar algumas técnicas mais básicas e no próximo falaremos de técnicas um pouco mais avançadas.

Em primeiro lugar vamos começar o Feature Engineering com o tratamento do dados faltantes, os valores nulos ou missing values.
Tratando valores faltantes
Imputar valores faltantes significa substituir esses valores por valores válidos, seguindo algum critério. Vamos apresentar alguns critérios mais comuns como média, mediana, moda ou um valor constante. Primeiramente vamos visualizar graficamente os nossos dados faltantes usando a biblioteca missingno.

Agora vamos ver como imputar valores, substituindo os dados nulos. Selecionamos a coluna TAX para exemplificar. Porém em alguns casos pode ser melhor para o modelo eliminar as observações com dados nulos, vamos ver um exemplo também.
Imputando a moda, média ou mediana
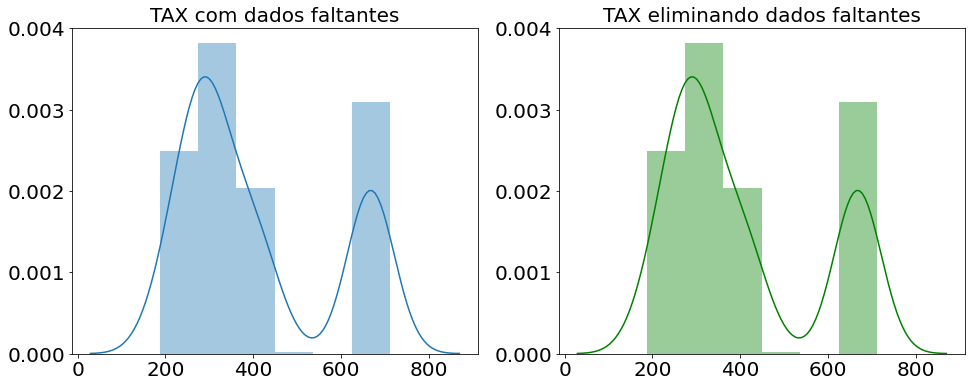
Geralmente se escolhe entre a média e a mediana, quando os valores são muito dispersos (usa-se a mediana) ou pouco dispersos (usa-se a média). No exemplo abaixo, usamos o dataset Boston que vem com a biblioteca scikit-learn. A figura da esquerda mostra a distribuição dos dados da variável TAX com os valores nulos e a figura da direita mostra a distribuição com a imputação da média.
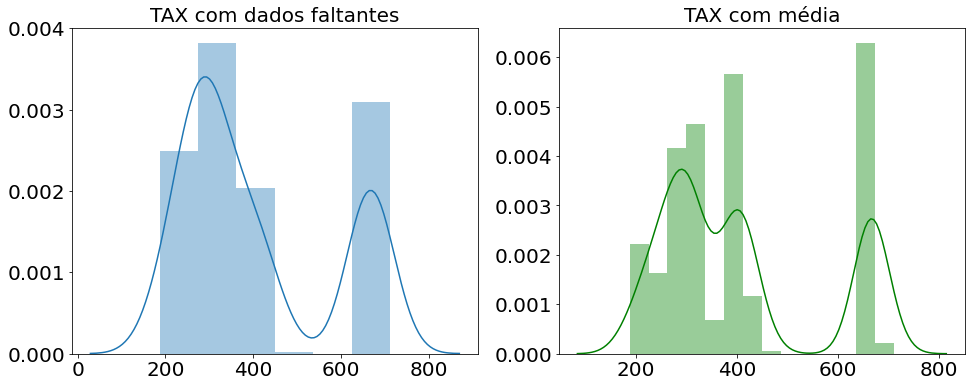
A figura abaixo apresenta de modo semelhante, porém com a mediana. Pode-se observar que há uma menor distorção na distribuição dos dados quando comparado à imputação pela média.
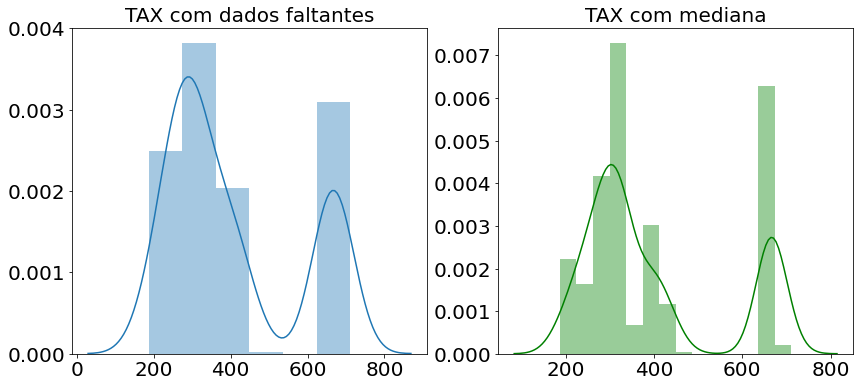
Já a moda geralmente se escolhe quando o valor mais frequente faz mais sentido para aqueles dados. No exemplo abaixo é possível observar que há uma distorção bem menor da distribuição dos dados.
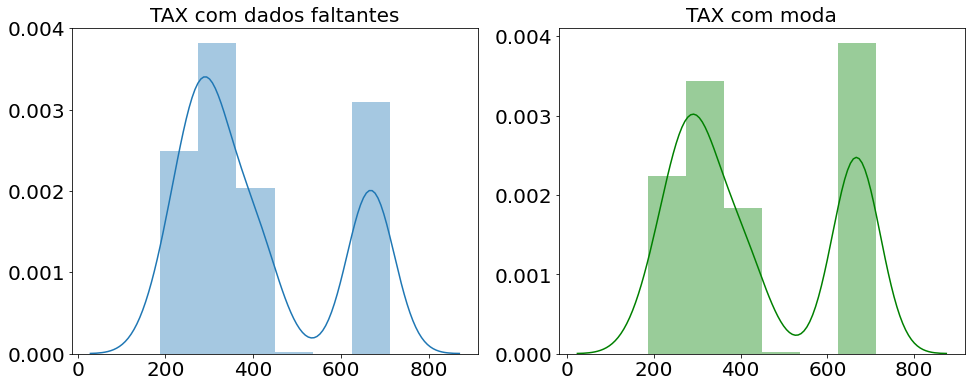
Imputando um valor constante
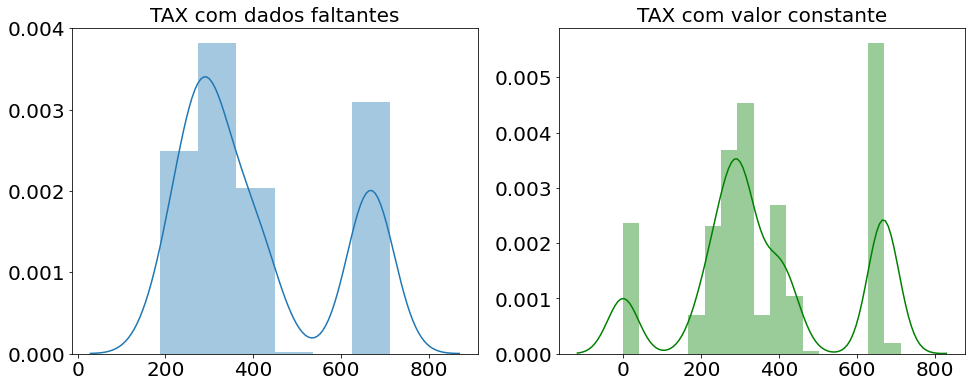
Os valores constantes podem ser imputados com duas razões diferentes: primeiro como uma flag que aquele valor é faltante (podendo também ser criada outra coluna para isso), e segundo como um valor que para aquele problema você acredita que faça mais sentido. No exemplo abaixo é possível observar que a imputação com o valor -1 provocou a criação de uma nova barra no gráfico, modificando a distribuição dos dados.
Eliminando observações com valores faltantes
Muitas vezes precisaremos eliminar as linhas ou colunas com muitos dados faltantes, pois preencher só confundirá o modelo. A porcentagem de dados faltantes necessária para se eliminar a linha ou coluna vai depender do problema a ser resolvido. Mas claro que se tiver 100% dos dados faltantes aquele dado não tem muita utilidade, mas para outros casos é necessário analisar o contexto.
Agora que aprendemos o que fazer com os dados faltantes do dataset, vamos ver o que fazer com as variáveis categóricas. Visto que para o input nos modelos os dados precisam ser numéricos. Agora vamos ver como tratar as variáveis categóricas.
Codificando variáveis categóricas
As variáveis do tipo categórica são as variáveis qualitativas, se não sabe do que estamos falando confere a explicação sobre os tipos de variáveis no post (Análise Exploratória de Dados com Python Parte I). Afinal vamos aprender as tecnicas One Hot e Ordinal para tratamento das variáveis categóricas.
One Hot
A codificação One Hot transforma uma coluna com K valores únicos em K colunas com valores 0 e 1, sendo 1 para presença e 0 para ausência daquele atributo.
Por exemplo eu tenho um atributo SEXO com valores Masculino e Feminino. Codificados como One Hot ficaria uma coluna Masculino com o valor 1 se o sexo for masculino e 0 caso contrário. Da mesma forma ocorre também com uma coluna Feminino. Sendo assim essa separação auxilia alguns algoritmos a identificarem melhor cada classe.
| Sexo | Sexo_Masculino | Sexo_Feminino |
| M | 1 | 0 |
| F | 0 | 1 |
Assim podemos observar o trecho de código abaixo que demonstra como utilizar a codificação One Hot no sklearn.
ohe = OneHotEncoder(sparse=False) ohe.fit(X[['AGE_discrete']]) age_one_hot = ohe.transform(X[['AGE_discrete']])
Ordinal
A codificação Ordinal muitas vezes é confundida com a Label pois são bem semelhantes na forma de agir, porém a Ordinal é mais indicada para os atributos e a Label mais indicada para o alvo (target), ou variável dependente.
Portanto a codificação Ordinal age atribuindo um valor numérico para cada valor único da coluna. Esses valores são incrementais (de 0 a K-1, onde K é a cardinalidade da coluna). Só que o problema é que alguns algoritmos podem interpretar que, por exemplo, o valor 2 é melhor do que um 1, ou seja, ele atribui uma ordenação do “pior” para o “melhor”. Isso pode acabar atrapalhando alguns algoritmos.
Abaixo um exemplo com uma variável hipotética Cidade. Podemos perceber que, ao primeiro é atribuído o valor 0, ao segundo 1 e assim por diante.
| Cidade | Cidade_Ordinal |
| São Paulo | 0 |
| Rio de Janeiro | 1 |
| Salvador | 2 |
Para utilizarmos a codificação Ordinal no scikit-learn, é bem semelhante aos outros transformadores, chama-se a função fit para ‘encaixar’ os dados, depois a função transform para transformar esses dados, ou pode-se chamar direto fit_transform caso for transformar apenas uma variável. Lembrem-se que se for transformar conjunto de treinamento e de teste, não dê fit no teste!
ord = OrdinalEncoder() ord.fit(X[['AGE_discrete']]) age_ordinal = ord.transform(X[['AGE_discrete']])
Agora que já aprendemos o que fazer com os dados faltantes e com as variáveis categóricas, vamos ver o que podemos fazer para tratar variáveis numéricas.
Transformando variáveis numéricas
Geralmente, para os algoritmos de aprendizado de máquina funcionarem com mais eficiência, é necessário normalizar os dados numa escala ou entre zero e um (usando MinMaxScaler) ou patronizar removendo a média e dividindo pela variância (usando StandardScaler). Também existem outros métodos como RobustScaler que serão detalhados em outra postagem.
MinMaxScaler
A normalização MinMaxScaler busca deixar os dados entre 0 e 1. Isso é necessário para “diminuir a distância” entre os valores, ajudando a melhorar o desempenho dos algoritmos. Abaixo como fazemos essa normalização com python.
mm = MinMaxScaler() mm.fit(X) X_minmax = mm.transform(X)
Abaixo um gráfico comparando antes de depois da normalização com MinMaxScaler.
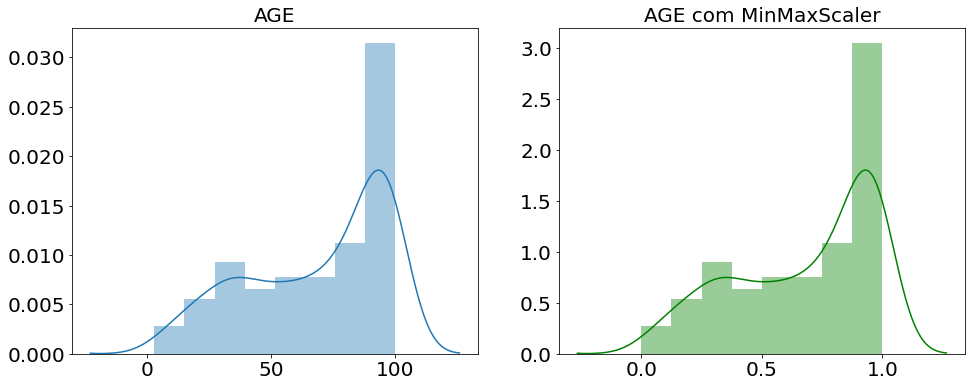
Podemos ver a mudança de escala tanto no eixo x quanto no eixo y efeito da normalização MinMaxScaler, agora vamos ver a padronização com StandardScaler.
StandardScaler
A padronização StandardScaler busca trazer todos os valores para um valor médio de 0 e um desvio padrão de 1. Vejam no código abaixo como fazemos essa padronização com python.
ss = StandardScalerScaler() ss.fit(X) X_sscaler = ss.transform(X)
Abaixo um gráfico comparando antes de depois da padronização com StandardScaler.
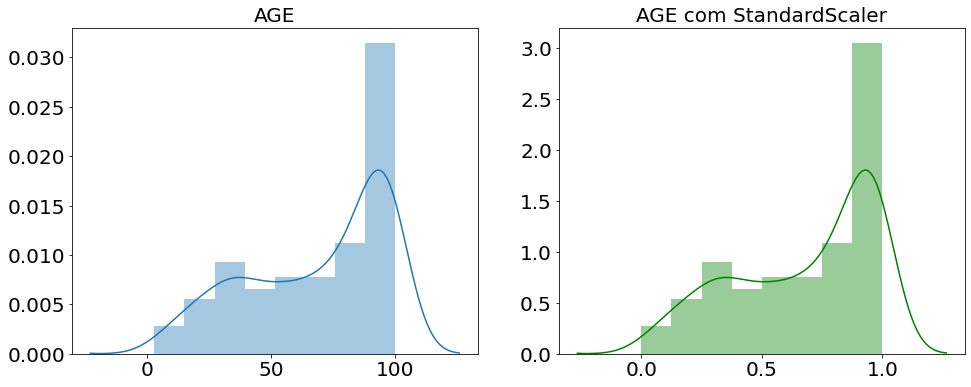
Podemos ver a mudança de escala tanto no eixo x quanto no eixo y efeito da padronização StandardScaler. Por fim, vamos ver o que podemos fazer para tratar os outliers.
Tratamento de outliers
Os outliers são dados fora do padrão, ou seja, valores atípicos que podem ser um erro. Dessa forma esses dados podem atrapalhar a análise dos dados, e aqui vamos ver duas formas de eliminar esses dados discrepantes. Podemos encontrar esses valores a partir do IQR ou do desvio padrão, além de outras técnicas, como z-score e winsonrizer, que serão abordados futuramente. Para saber mais sobre essas e outras medidas estatísticas veja o post (Estatística Descritiva Univariada)
Intervalo Interquartil (IQR)
O Intervalo Interquartil pode ser utilizado no tratamento de outliers, através da técnica de “aparar” (trimming). Essa técnica substitui todos os valores acima ou abaixo de um certo valor pelo valor limite. A função abaixo utiliza essa técnica:
def remove_outliers_iqr(col, pct=1.5):
Q1, Q3 = col.quantile([0.25,0.75])
IQR = Q3 - Q1
inf = Q1 - pct*IQR
sup = Q3 + pct*IQR
return np.where(col < inf, inf, np.where(col > sup), sup, col)Desvio padrão
Para remoção de outliers, geralmente é utilizado o intervalo de 3 desvios padrões pra esquerda e para a direita para detectar e aparar os outliers. Podemos ver na figura abaixo uma distribuição normal e onde ficam localizados os seus desvios padrões multiplicados por 1 até 4. Podemos observar que se os dados são maiores que 3 desvios padrões, tem uma possibilidade boa de serem outliers! Mas nem sempre, é sempre necessário analisar o contexto.
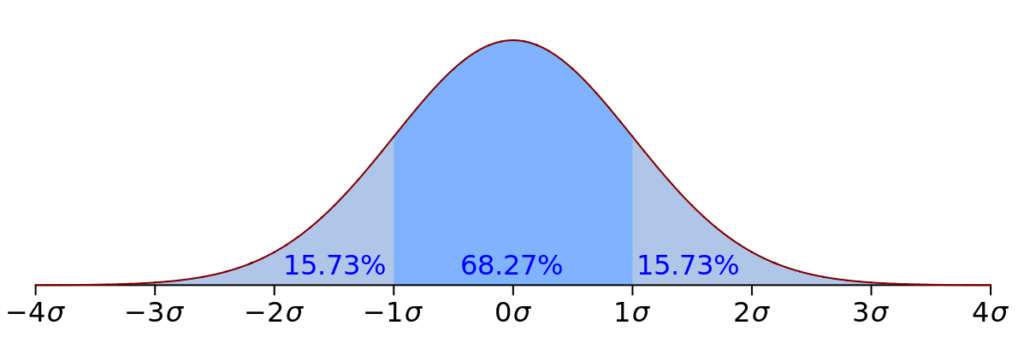
A função abaixo realiza a remoção de outliers utilizando o desvio padrão.
def remove_outliers_std(col):
std = col.std()
mean = col.mean()
lim = 3*std
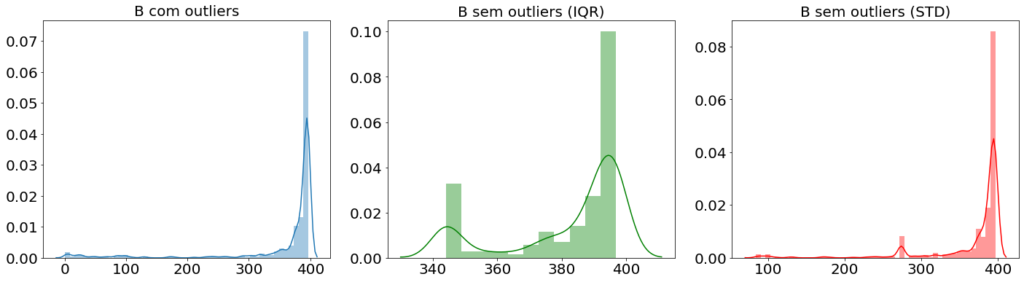
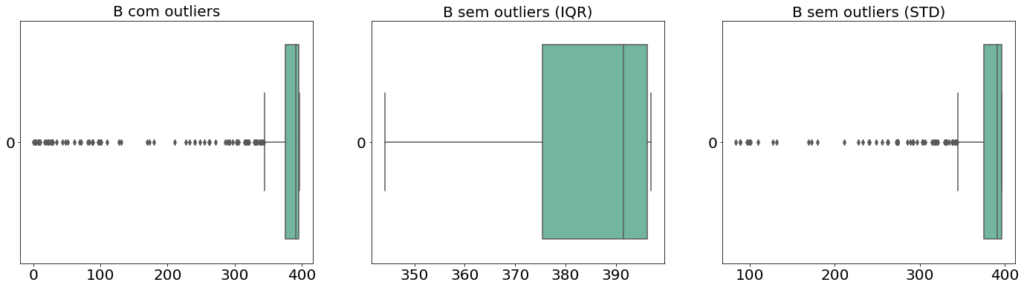
return np.where(col < mean - lim, lim, np.where(col > mean + lim), lim, col)Observem que as imagens abaixo mostram o tratamento de outliers na variável B do dataset Boston. É possível observar que, aplicando as duas técnicas acima, a técnica de IQR proporciona uma melhor remoção de outliers, enquanto a técnica de STD (desvio padrão) provoca uma menor alteração na distribuição dos dados.
Feature Engineering ao Cubo
É isso sobre Feature Engineering por hoje! Foi muito bom estar aqui com vocês, e quem quiser dar uma olhada em um pouco de código só acessar o Jupyter Notebook no GitHub. Vamos ter outros post para aprofundar no tem engenharia de atributos que é tão importante para a ciência de dados.

– “Sim, você joga os dados nessa grande pilha de álgebra linear e coleta as respostas do outro lado.”
– “E se as respostas tiverem erradas?”
– “Apenas mexa na pilha até começarem a parecer certas”
Fonte: xkcd.com
Referências de Feature Engineering
Conteúdos ao Cubo
Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.
- NLP com scikit-learn
- Classificação com scikit-learn
- Agrupamento com scikit-learn
- Previsão de Séries Temporais com SKTime
- Sistemas de Recomendações com Surprise
- Variáveis em Python
- Extrair Dados da API do Cartola FC
- Organização de Arquivos e Pastas com Python
Então, finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades.

Programador e cozinheiro. Formado pela Universidade Federal do Piauí e com um mestrado (interrompido) pela UFRGS. Com uma grande sede de conhecimento, está sempre se perguntando os porquês e tentando dar o melhor naquilo que faz. Desde pequeno diz que vai ser cientista, seja da computação, de dados ou na cozinha. O conhecimento é a única esperança.
“Um homem não é outra coisa senão o que faz de si mesmo.” Sartre


