Python

Geometria Analítica com SymPy

On 22 de julho de 2020, by Cairo Rocha

Olá pessoas, aqui quem fala é o Cairo e vamos embarcar numa curta jornada sobre Geometria Analítica com SymPy. “Mas, Cairo, onde que eu vou utilizar isso? Eu só quero vender minha arte na praia, ops, ser um cientista de dados.“. Confia, mais a frente nós vamos precisar disso pra entender as próximas postagens sobre decomposição de matrizes e cálculo vetorial. Portanto vamos conhecer alguns conceitos importantes da geometria analítica.

O que é SymPy?

Em primeiro lugar vamos conhecer uma ferramenta para nos auxiliar nesse estudo. O SymPy é uma biblioteca em Python para matemática simbólica (uso de computadores para manipular equações matemáticas e expressões em forma simbólica, ou seja, contrário de numérica) . É uma biblioteca de software livre e vai desde a aritmética simbólica básica, cálculo, álgebra, matemática discreta e física quântica. Ela também é capaz de formatar os resultados em código LaTeX.

Devidamente apresentados ao SymPy, agora vamos ao nosso primeiro conceito da geometria analítica, a norma.

Norma

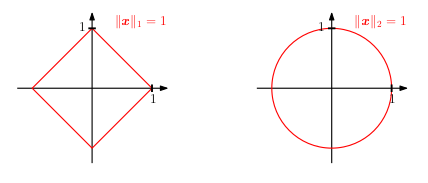
A norma de um vetor x é uma função que atribui a cada vetor a sua distância . As normas mais conhecidas são a de Manhattan e a Euclidiana, que calculam as respectivas distância de Manhattan e distância euclidiana. Enquanto a distância de Manhattan (1) é a soma dos valores absolutos, a distância euclidiana (2) é a soma dos valores ao quadrado tirado a raiz quadrada. A figura acima mostra melhor a relação dos valores para vetores com norma igual a 1.

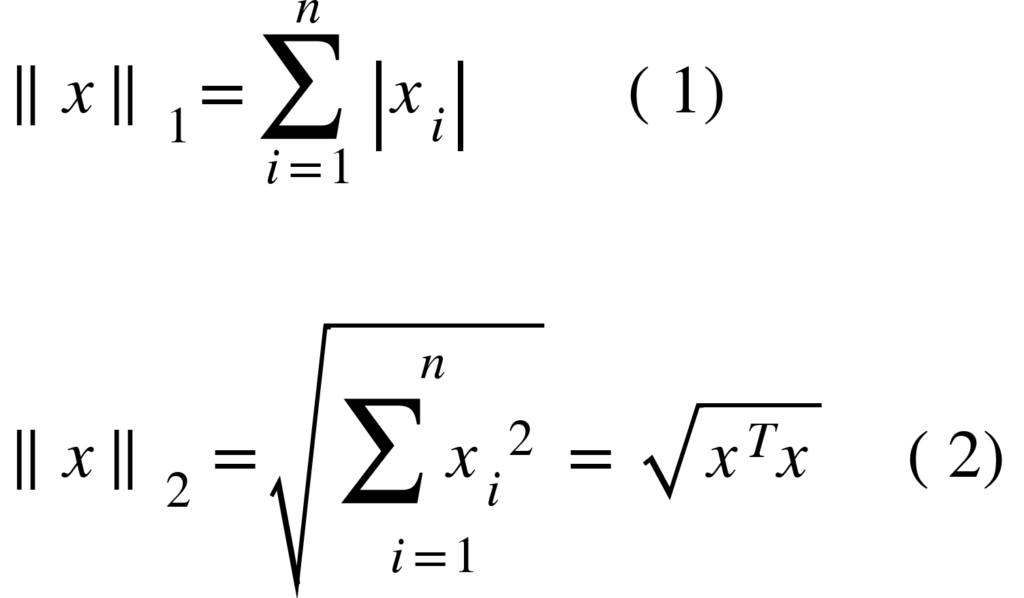
Assim vamos ver como aplicar esse conceito com o SymPy.

Aplicação da norma no SymPy

Para matrizes, é utilizada a norma de Frobenius ou norma matricial, que é uma extensão da norma euclidiana para matrizes. Ela é calculada aplicando a função norm a uma matrix. Para retornar o resultado numérico, basta chamar a função evalf.

from sympy.matrices import Matrix

a = Matrix([[3, 2, 1],[0, 2, 3]])
a
Matrix([
[3, 2, 1],
[0, 2, 3]])
a.norm()
3*sqrt(3)
n = a.norm()
n.evalf()
5.19615242270663

Agora que já estamos entendidos com a norma, podemos seguir para as matrizes simétricas positivas definidas.

Matriz simétrica positiva definida

Uma matriz é chamada de simétrica positiva definida, ou só matriz positiva definida, quando satisfaz (3):

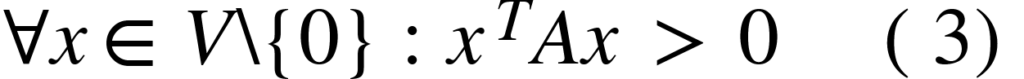
“O que??”. Calma, vamos devagarzinho. Lê-se “para todo x pertencente a V (espaço vetorial), x transposta vezes A vezes x é maior que 0”. Caso for é chamada semidefinida. No exemplo vai ficar mais tranquilo:

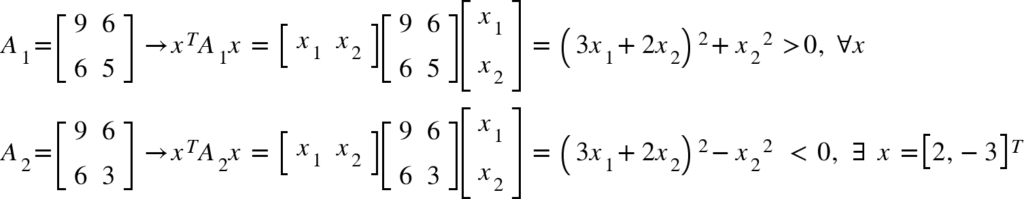
Podemos notar que, aplicada a fórmula, enquanto o primeiro exemplo é sempre positivo, o segundo exemplo existe x onde o valor é menor que 0. Então apenas a primeira é uma matriz positiva definida.

Mas eu consigo aplicar esse conceito usando o SymPy? Claro!

Matriz positiva definida no SymPy

Abaixo segue o exemplo acima traduzido para código SymPy. Como podem ver é uma tradução bem direta. A função simplify “simplifica” a função aplicando algumas regras, enquanto a função factor fatora um polinômio em fatores irredutíveis. Mas como podem observar, nenhum deles chegou no resultado que precisávamos.

from sympy.matrices import Matrix
from sympy import simplify, Symbol, factor

x1= Symbol('x1')
x2 = Symbol('x2')
x = Matrix([x1,x2])
x
Matrix([
[x1],
[x2]])
A1 = Matrix([[9,6],[6,5]])
d = x.T*A1*x
Matrix([[x1*(9*x1 + 6*x2) + x2*(6*x1 + 5*x2)]])
simplify(d)
Matrix([[9*x1**2 + 12*x1*x2 + 5*x2**2]])
factor(d)
Matrix([[x1*(9*x1 + 6*x2) + x2*(6*x1 + 5*x2)]])

Agora que já estamos entendidos com a norma e conhecemos a matriz simétrica positiva definida, então estamos prontos para entender sobre os ângulos e ortogonalidade.

Ângulos e ortogonalidade

Existe definido como o ângulo entre x e y, tal que:

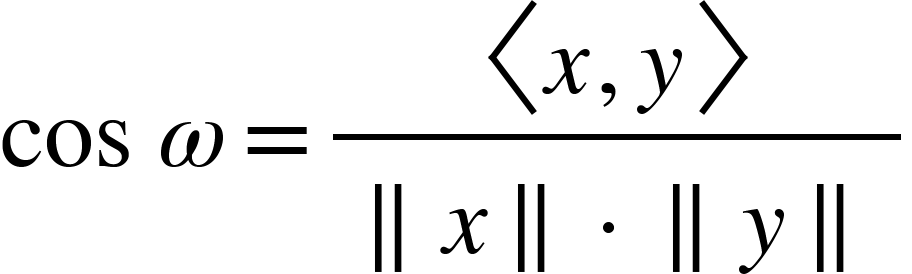
Onde <x,y> é o produto interno de x e y e ||x|| é a norma euclidiana. Vamos pro exemplo:

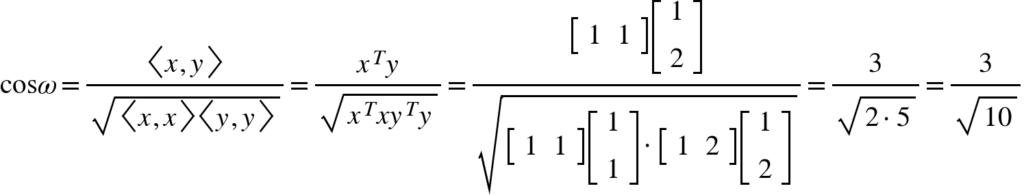
Vetores ortogonais: Dois vetores são ortogonais se . Caso também aconteça que ||x|| = ||y|| = 1, dizemos que esses dois vetores são ortonormais. Para ortogonalizar um conjunto de vetores, usamos o método de Gram-Schmidt.

Mas o python já tem biblioteca pronta para isso também? Sim! Vamos ver no SymPy como fica.

Ângulos e vetores ortogonais em SymPy

Por exemplo, podemos calcular o coseno do ângulo de forma bem direta, usando o produto interno através da função dot. O SymPy também já vem com o método de Gram-Schmidt implementado, gerando matrizes ortogonais. É só passar como argumento a lista de matrizes.

x = Matrix([[1],[1]])
y = Matrix([[1],[2]])
x.T.dot(y)/sqrt(x.T.dot(x)*y.T.dot(y))
3*sqrt(10)/10
GramSchmidt([x,y])
[Matrix([
[1],
[1]]), Matrix([
[-1/2],
[ 1/2]])]

O método de Gram-Schmidt utiliza projeções para transformar qualquer base de um espaço vetorial n-dimensional em uma base ortogonal/ortonormal. Então vamos a seguir falar um poucos dessas projeções.

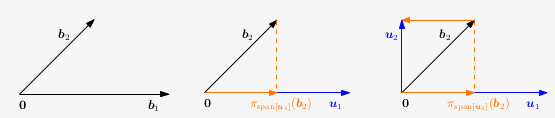
Transformando uma base não-ortogonal em uma base ortogonal (u¹, u²)

Projeções ortogonais

Projeções são uma classe importante de transformações lineares, e tem um papel importante em gráficos, teoria dos códigos, estatística e aprendizado de máquina. No aprendizado de máquina as projeções podem servir para, por exemplo, redução de dimensionalidade. Dois algoritmos que podem executar essa redução são o PCA (Principal Component Analysis – Análise de Componentes Principais)e os Autoencoders.

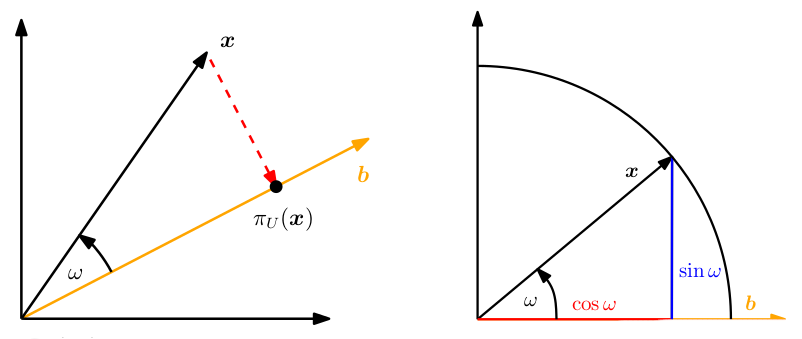
Uma projeção ortogonal pode ser sobre uma reta, sobre um plano, etc. A projeção ortogonal sobre um plano pode ser comparada à sombra desse mesmo objeto no horário em que o sol está mais alto no dia. Nesse horário, a sombra possui dimensões iguais às do objeto, mas não possui profundidade alguma.

Assim também podemos aplicar estes conceitos com o SymPy, vejamos.

Projeções ortogonais em SymPy

Utilizando o sympy, podemos obter a projeção ortogonal através da função project da matriz passando como argumento sobre qual plano pretende fazer a projeção.

from sympy import Matrix, sqrt

V = Matrix([sqrt(3)/2, 1/2])
x = Matrix([[1, 0]])
V.project(x)
Matrix([[sqrt(3)/2, 0]])

Por fim, vamos falar das rotações para fechar esse conceitos sobre a geometria analítica.

Rotações

Rotações são mapeamentos lineares que rotaciona um plano por um ângulo em relação a origem. A rotação é muito importante em áreas como computação gráfica e robótica, como por exemplo saber a rotação que precisamos fazer para rotacionar um braço robótico. Então, temos a equação abaixo define a matriz de rotação em relação ao sistema padrão de coordenadas em .

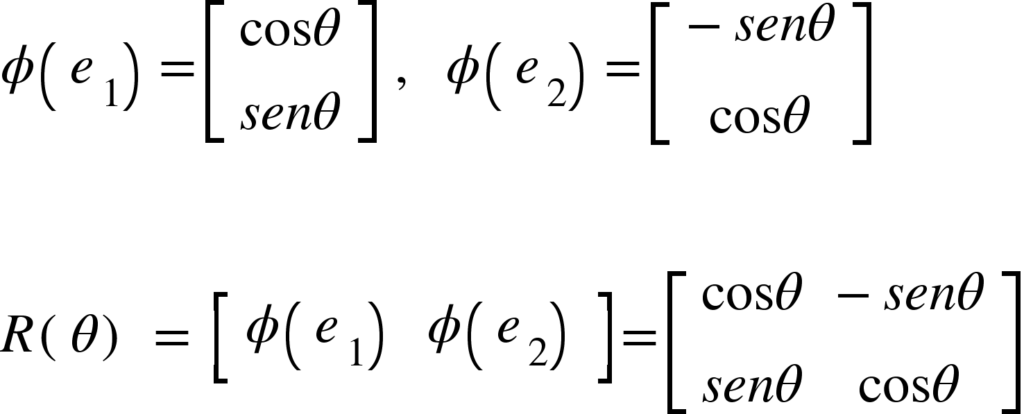
De acordo com os conceitos acima vamos ver como aplicar com o SymPy.

Rotações em SymPy

No SymPy, temos as funções rot_axis1, rot_axis2 e rot_axis3 para rotacionar no primeiro, segundo e terceiro eixo, respectivamente. Veja abaixo como utilizar as funções rotacionando nos eixos 1 e 2:

from sympy import pi
from sympy.matrices import rot_axis1, rot_axis2

theta = pi/3
rot_axis1(theta)
Matrix([
[1,          0,         0],
[0,        1/2, sqrt(3)/2],
[0, -sqrt(3)/2,       1/2]])
rot_axis2(theta)
Matrix([
[      1/2, 0, -sqrt(3)/2],
[        0, 1,          0],
[sqrt(3)/2, 0,        1/2]])
rot_axis2(pi/2) # 90º
Matrix([
[0, 0, -1],
[0, 1,  0],
[1, 0,  0]])

Geometria Analítica com SymPy ao Cubo

Enfim, por hoje é só, pe-pessoal. Sendo assim, abaixo algumas referências pra vocês e um tutorialzinho do SymPy. Abraços e até a próxima!

Mas não esquece de deixar um feedback aí nos comentários ou se preferir manda uma mensagem para o Dados ao Cubo.

Referências de Geometria Analítica

Conteúdos ao Cubo

Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.

Finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades.

Cairo Rocha

Programador e cozinheiro. Formado pela Universidade Federal do Piauí e com um mestrado (interrompido) pela UFRGS. Com uma grande sede de conhecimento, está sempre se perguntando os porquês e tentando dar o melhor naquilo que faz. Desde pequeno diz que vai ser cientista, seja da computação, de dados ou na cozinha. O conhecimento é a única esperança.

“Um homem não é outra coisa senão o que faz de si mesmo.” Sartre

Gostou? Compartilhe!