Entre Vieses e Causalidades: Como (não) ser Enganado pelos Dados

Falaa galera! Hoje mais um postzinho mais teórico pra quem for de teoria. Vamos falar de viés (o famoso bias) e causalidade (a famosa causalidade mesmo). Se você tá me xingando mentalmente falando que viés é minha mãe, você precisa urgentemente desse post. Quenhé esse viés, causalidade, é o que vamos aprender na seção abaixo.

Introdução a Viés e Causalidade

Primeiramente vamos entender o conceito de viés e causalidade, em seguida vamos aprofundar um pouco mais. Dessa forma iremos entender como esses conceitos impactam na análise de dados.

Viés

Viés ou tendência é um peso desproporcional a favor ou contra uma coisa, pessoa ou grupo comparado a outro, geralmente de uma maneira considerada injusta. Para nós, cientistas de dados, são simplesmente dados tendenciosos a confirmar uma hipótese de forma parcial onde alguém sai ganhando algo nisso. 

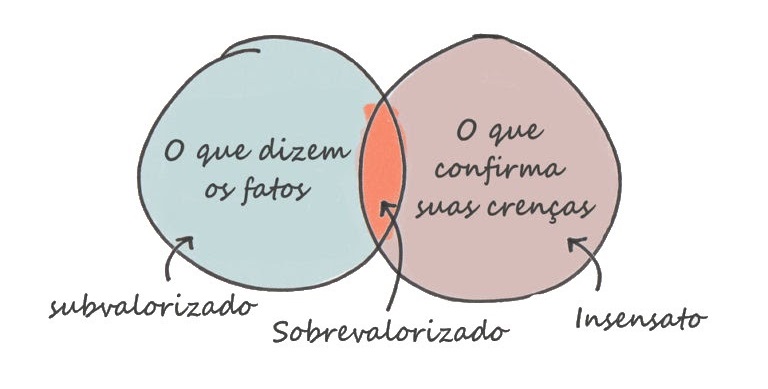
Analisando a figura abaixo, podemos observar que algumas pessoas (talvez a grande maioria) só valoriza os fatos caso esses confirmem suas crenças, então essa informação é enviesada, como por exemplo a vacina que está chegando e causando polêmica no mundo todo.

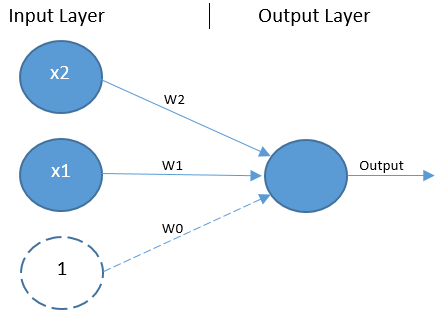
Outro exemplo de transposição do viés para o mundo dos dados é nas redes neurais, onde o bias representa um nó da rede que sempre entra com o valor 1. Mas pra que mesmo? Imagina que tu tem um problema de AND ou OR (relembrando, AND é quando a saída é 1 quando as duas entradas são iguais a 1, e OR é quando a saída é 1 quando pelo menos uma das entradas é 1), linearmente separáveis, e inserimos um nó com o viés (bias).

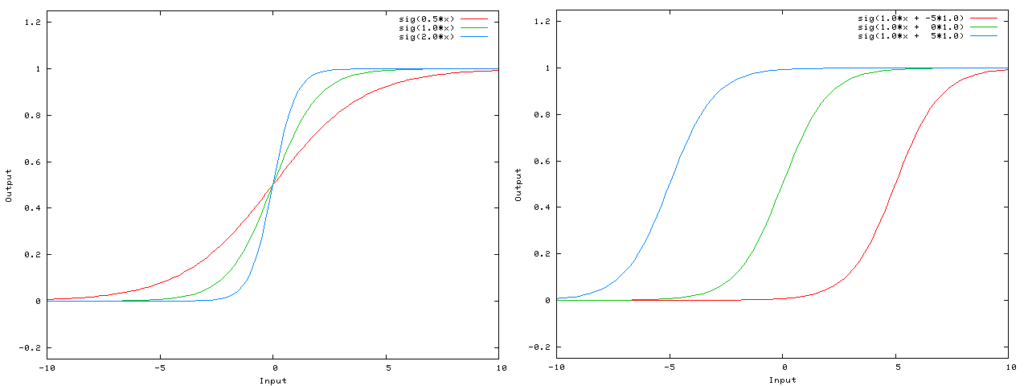
Na figura abaixo conseguimos ver o efeito dessa adição. Na figura da esquerda, sem bias, a função de ativação é uma sigmóide (mas nesse caso mais simples pode ser uma função degrau) é igual a x1*w1 + x2*w2, onde w1 e w2 são os pesos, isso faz com que, em algum momento, a função sempre passa pelo ponto 0. Já na figura da direita, a função se torna x1*w1 + x2*w2 + w0*1, fazendo com que haja uma separação maior entre entrada e saída dos dados, permitindo atingir um maior espaço de busca.

Causalidade

A causalidade, na sua forma mais simplificada, é a relação entre dois eventos A e B, onde A causa B, ou seja, B ocorre apenas caso A tenha ocorrido. Essa é a simplificação da simplificação pois é um assunto muito amplo, onde por exemplo B ocorre caso A ocorra, mas não somente. 

Existem modelos de causalidade de diversas áreas, desde humanas à exatas, passando pelo senso comum e até as causas de Aristóteles. Mas vamos focar na Ciência de Dados por enquanto, analisando o seguinte diagrama causal:

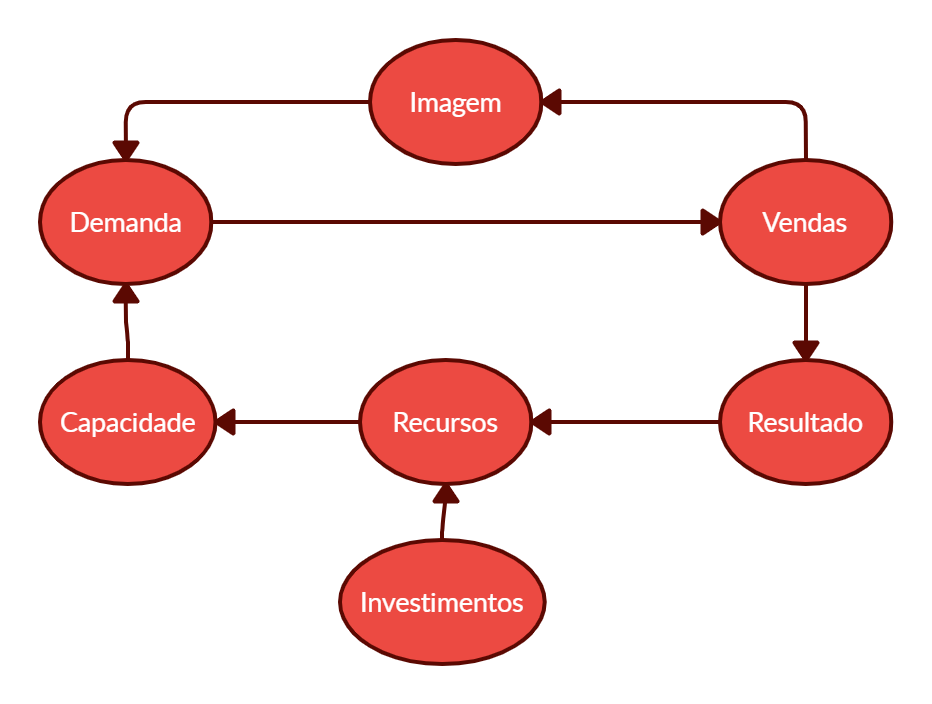
Um diagrama causal é um diagrama que auxilia na visualização das causas. No diagrama de exemplo acima, temos que a causa de existirem Recursos é a existência de Investimentos. Do mesmo modo, para existir Demanda, é necessário uma boa Imagem da empresa (que por sua vez depende das Vendas) e uma boa Capacidade de produção (para existir oferta do produto), que por sua vez depende dos Recursos! 

Sacaram já, né? Senão retorne pro início desse parágrafo e dê uma olhada no diagrama com carinho. Quando o loop encerrar, vamos pra próxima sessão que vai falar de algumas extensões da causalidade e viés, como a Falácia ecológica, Precificação dinâmica e Viés de seleção.

Falácia ecológica

 Aqui o problema se dá ao analisar variáveis agregadas e fazer suposições sobre os dados desagregados, ou seja, olhar o macro e deduzir o micro.

Um exemplo de falácia ecológica é o Paradoxo de Robinson  (deduzir correlações de um grupo a partir de correlações populacionais). Em 1950, Robinson encontrou que quanto maior a proporção de imigrantes de um estado americano, menor era a taxa de analfabetismo. Porém, a nível individual, os imigrantes eram menos alfabetizados que os nativos. Ele provou matematicamente que a covariância total de duas variáveis pode ser expressa como o somatório de um componente intragrupo e um componente intergrupo (ecológico). 

Paradoxo de Simpson

O paradoxo de Simpson pode ser considerado um caso específico da falácia ecológica. É um paradoxo onde um conjunto de dados completo aponta em uma direção, mas uma análise de subconjuntos aponta na direção contrária. 

Por exemplo, em 1973 na Universidade da Califórnia buscou-se entender um suposto viés de gênero na admissão dos cursos de pós-graduação da universidade. Dentre os candidatos, haviam cerca de 8000 homens e 4000 mulheres. Enquanto 44% dos homens eram admitidos, apenas 35% das mulheres eram admitidas. Com os dados agrupados e corrigidos, um pequeno viés em favor das mulheres aparece. A conclusão do trabalho foi que as mulheres se inscreviam mais em departamentos concorridos, como o Departamento de Inglês, enquanto os homens optaram por departamentos onde era mais fácil ser admitido, como Química e Engenharia.

Intervenção e Precificação dinâmica

Se seu algoritmo de Machine Learning faz uma predição e não afeta a realidade (como será que choverá amanhã?), intervenção não é algo a se preocupar. Mas se seu algoritmo produz insumo para o business gerar uma ação de como alterar o desconto que um cliente terá direito para maximizar sua probabilidade de compra, você tem que levar em conta a reação do cliente ao treinar o seu modelo.

Na precificação dinâmica, preços e descontos históricos geralmente não são um bom indicativo do que será um bom preço / desconto futuro, pois quem disse que aquele valor futuro era um valor ótimo?

Uma das formas de contornar esse problema é o algoritmo abaixo, conhecido como multi-arm bandit.

Problema das Roletas de k Alavancas

O Problema da Roleta de k Alavancas é uma extensão do famoso teste A/B para mais de 2 variáveis. Não conhece o teste A/B? Vamos dar uma olhadinha na Wikipédia:

Teste A/B é um método de teste de design através do qual comparam-se elementos aleatórios com duas variantes, A e B, em que estes são o controle e o tratamento de uma experiência controlada, com o objetivo de melhorar a percentagem de aprovação.

Imagine que um polvo vá a um cassino, e nele se depare com uma roleta com 8 (ou um número qualquer) alavancas. Cada alavanca tem uma certa chance de devolver uma certa quantidade de dinheiro, na média algumas alavancas devolvem mais dinheiro do que outras. O objetivo do polvo é aprender, a partir de Aprendizado por Reforço, a puxar a alavanca que mais lhe devolve dinheiro.

Mas como? Se o polvo soubesse os valores esperados, ele sempre puxaria a alavanca que retornasse o maior valor, certo? Mas nesse caso, ele sempre recebe um valor dentro de uma distribuição probabilística, então tem que utilizar duas técnicas famosas em estudos de pesquisa operacional e metaheurísticas: a exploração e a explotação.:

Exploração: Explorar nesse caso significa ir cada vez mais fundo para tentar encontrar a melhor solução, por exemplo sempre ir pelo valor ótimo da última iteração. O problema disso é ficar preso em valores subótimos, os chamados ótimos locais.

Explotação: Explotação já seria quando queremos andar em novas áreas, ou seja, conhecer outras possibilidades de resultados para depois (talvez realizando uma exploração), tentar encontrar o resultado do ótimo global (o melhor resultado possível).

Viés de Seleção

Viés de seleção tem a ver com como escolhemos nossos dados. Por exemplo, se queremos medir a eficiência de um curso no aumento de produtividade dos funcionários de uma empresa. Nesse caso, vamos precisar selecionar uma amostra caso o curso não possa ser ministrado a todos os funcionários. 

Essa amostra tem que ser representativa dos dados e existem algumas técnicas de amostragem estatística que podem ajudar a resolver esse problema. Mas suponha que o gestor não sabe isso, e selecione os 50 primeiros que responderam ao email da convocação. Ele gerou um viés de seleção, pois a amostra está enviesada no fato de que provavelmente quem se matriculou no curso são os mais interessados e mais atentos da empresa.

Um problema muito famoso desse tipo de viés é o problema do Dr. Wald. Na Segunda Guerra Mundial, retornavam muitos aviões baleados, e era preciso saber onde blindar esses aviões, pois caso blindassem todo o avião, além do custo ele ficaria muito pesado.

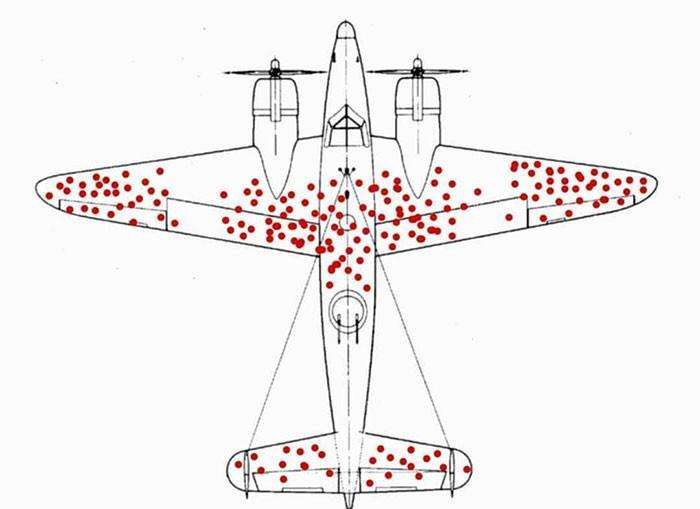
O Dr. Wald percebeu que não adiantaria blindar os pontos onde o avião tinha marcas de bala, pois esses pontos provavelmente eram os mais resistentes, pois esses aviões conseguiram retornar à base! A sacada foi exatamente blindar onde não existiam vestígios de bala, pois essa área foi provavelmente onde os aviões que não retornaram foram atingidos!

Viés e Causalidade ao Cubo

Cuidado com como você utiliza os dados da empresa em que você trabalha. Faça uma análise detalhada para não cair nas ciladas apresentadas acima, pois caso contrário você pode acabar prejudicando a empresa com informações mal interpretadas.

Bem, essa foi apenas uma introdução ao tema de Viés e Causalidade, quem tiver interesse deixei alguns links abaixo onde podem buscar mais informações! 

Abraços, curtam, compartilhem, coloquem no slide de natal da família!

Referências sobre Viés e Causalidade

• 10 Coisas que você precisa saber sobre Viés e Causalidade
• Sua Primeira IA: o Problema dos k-Armed Bandits
• Paradoxo de Simpson
• Pensamento contrafactual e raciocínio causal
• Falácia ecológica
• O Ecológico na epidemiologia
• Seus resultados fazem sentido?
• What is the role of the bias in neural networks?

Conteúdos ao Cubo

Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.

• AutoML (Automated Machine Learning) com ML.Net
• DataViz com Power BI
• Sistemas de Recomendações com Surprise
• Inteligência Artificial em Ressonância Magnética
• Ciência de Dados para Mercado de Ações Parte I
• Ciência de Dados para Mercado de Ações Parte II
• Funções em Python
• Análise de Dados com Seaborn Python

Finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades.