Como vimos na Engenharia de Atributos AKA Feature Engineering Parte I, a Engenharia de Atributos é essencial para obtenção de um bom resultado de predição, pois ela vai auxiliar o algoritmo a entender melhor os padrões nos dados. Tá tudo muito bem, tá tudo muito bom, mas realmente… existem mais algumas técnicas bacanas um pouco mais avançadas que podemos utilizar!
Portanto vamos ver técnicas para dados faltantes, como codificar variáveis categóricas, técnicas de padronização dos dados, como realizar discretização de variáveis numéricas e por fim como tratar outliers.
Dados Faltantes
Indicador de Valores Faltantes
É uma prática comum colocar um indicador para se o dado é (1) ou não faltante (0). Isso ajuda a saber se aquele dado estava com valor nulo aleatoriamente (o algoritmo vai reconhecer o valor que substituiu ) ou não (o algoritmo vai reconhecer a flag de dado faltando 0 ou 1). Em python podemos acrescentar essa informação usando o método where do pandas ou do numpy (que eu prefiro por ser mais completo).
df['A_faltante'] = np.where( df['A].isna(), 1, 0)
Traduzindo, “Crie uma nova coluna com o valor igual a: onde o valor de A for nulo coloque 1 e onde não for coloque 0”.
KNNImputer
A classe KNNImputer substitui os valores nulos utilizando o algoritmo KNN (K Nearest Neighbors – K Vizinhos mais Próximos). Pra quem não conhece (e pra quem conhece também), o algoritmo KNN funciona escolhendo os K Vizinhos mais Próximos (ba dum tss)! Brincadeira, ele seleciona os k vizinhos através de uma medida de distância, geralmente a distância euclidiana.
O KNNImputer trabalha de forma semelhante, mas substituindo os valores nulos pela média dos k vizinhos mais próximos. Por padrão ele utiliza os 5 vizinhos mais próximos. O algoritmo abaixo mostra a utilização dessa técnica. Também é possivel fazer fit e transform separados, caso precise-se aplicar para mais de um conjunto de dados, apenas lembre de só dar fit nos dados de treino.
cols = train.select_dtypes('number').columns
knn = KNNImputer()
train[cols] = knn.fit_transform(train[cols])Codificando variáveis categóricas
Mean Encoding
A mean encoding ou target encoding como os próprios nomes já dizem, codificam as variáveis categóricas em numéricas, utilizando a média da variável em relação ao alvo (variável Y). Essa codificação só funciona para métodos supervisionados. Como a ordinal encoding pode passar a idéia que a variável 3 é melhor que a 2, ou a 4 é melhor que a 3… e assim por diante, a codificação mean quer que isso aconteça, pois quanto mais alto o valor melhor chance de encontrar valores do alvo igual a 1.
O exemplo abaixo demonstra essa técnica no dataset Titanic. Logo abaixo há uma tabela demonstrando melhor como funcionaria a técnica.
mean_encoder = ce.MeanCategoricalEncoder(variables='Embarked') train_mean = mean_encoder.fit_transform(titanic, titanic['Survived'])
| Variável | Mean Encoding | Alvo |
| A | 1/7 = 0.1428 | 1 |
| B | 0 | 0 |
| C | 2/7 = 0.2857 | 1 |
| A | 1/7 = 0.1428 | 0 |
| C | 2/7 = 0.2857 | 0 |
| C | 2/7 = 0.2857 | 1 |
Rare Labels
Rare labels ou rótulos raros são valores que aparecem muito poucas vezes na coluna. Nesse caso, podemos determinar um limite (por exemplo 5%) e tudo que for abaixo daquele limite se transformar em uma nova categoria chamada, por exemplo, “Other”.
titles = titanic['Name'].apply(lambda x: x.split(',')[1].split('.')[0])
count = titles.value_counts()
titles = np.where(count < 3, 'Other', count.index)Weight of Evidence
O Weight of Evidence (peso da evidência, em tradução livre) ou WoE codifica a variável utilizando a seguinte fórmula:
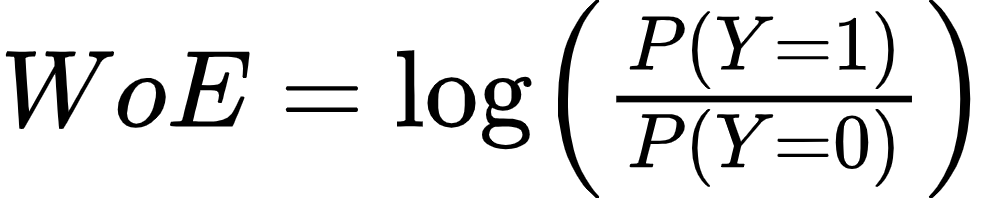
Onde P(Y=1) é a probabilidade do evento ocorrer. É semelhante ao Mean Encoding porém utiliza o logaritmo e não utiliza apenas quando o valor é igual a 1.
woe_encoder = ce.WoERatioCategoricalEncoder(variables='Sex') train_woe = woe_encoder.fit_transform(titanic, titanic['Survived'])
Padronização
Robust Scaler
É semelhante a normalização, porém utiliza o intervalo interquartil, sendo mais robusto (daí o nome) à outliers.
rs = RobustScaler()
train_cp = train.copy(deep=True)
train_num = train.select_dtypes('number').columns
train_cp[train_num] = rs.fit_transform(train[train_num])Log Transform
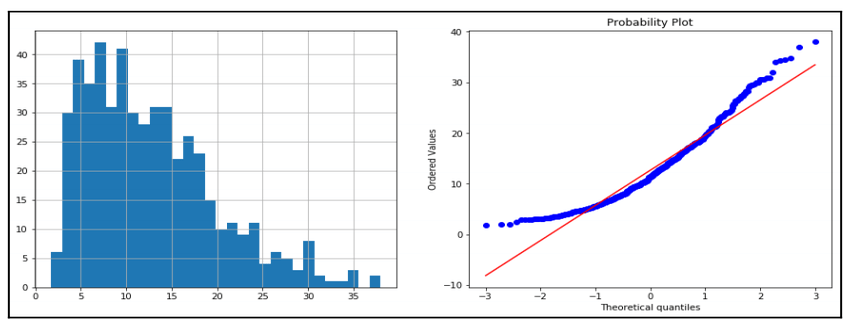
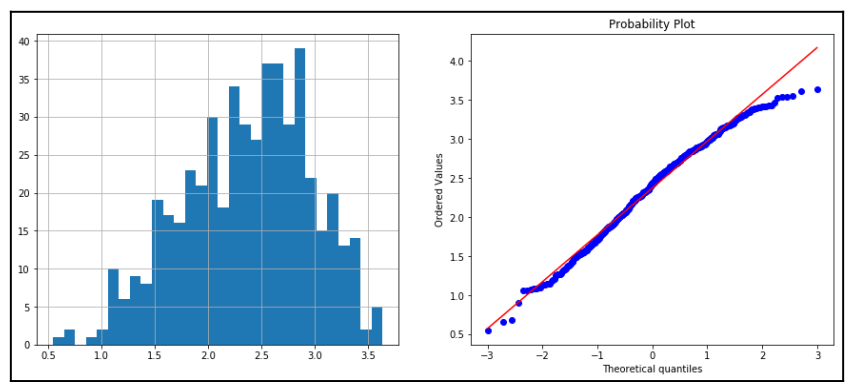
A transformação logarítmica é bem comum de ser executada quando queremos que a coluna tenha uma distribuição normal. É importante lembrar que essa transformação só pode ser aplicada a valores positivos.
train_cp = train.copy(deep=True) train_cp[train_num] = np.log(train[train_num])
Abaixo o exemplo da distribuição e QQ Plot de uma variável antes e depois do log transform. Podemos notar uma menor assimetria e maior semelhança com uma distribuição normal. O QQ Plot mais centralizado na diagonal principal é uma evidência que essa variável se aproximou mais de uma distribuição normal.
Box-Cox
A transformação Box-Cox pertence a uma classe de funções da família da potenciação. Nessa transformação, existe um fator lambda que é otimizado para aproximar a distribuição da função a uma normal. Porque estou insistindo nisso de aproximar de uma normal? Porque fica mais fácil de resolver com algoritmos lineares o problema. Abaixo a função dessa transformação:
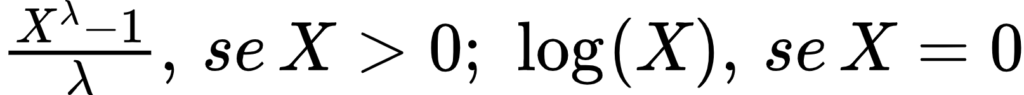
Abaixo, aplicando essa técnica à variável LotFrontage do dataset House Prices do Kaggle. A função retorna a Series transformada e o parâmetro lambda.
train_cp = train.copy(deep=True) train_cp['LotFrontage'], param = stats.boxcox(train['LotFrontage'])
A transformação Box-Cox só funciona em variáveis positivas. Caso queira utilizar em variáveis com valores zero ou negativos, há uma extensão chamada Yeo-Johnson.
Discretização de Variáveis Numéricas
Existem diversos métodos que fazem a discretização (transformar valores contínuos em numéricos) de variáveis numéricas, podendo ser discretizadas por valores ou por frequência, mas hoje veremos um método um pouco diferente, discretização usando o K-Means.
K-Means
O algoritmo de clusterização (agrupamento) K-Means pode ser utilizado para discretizar os valores de uma variável. Ele agrupa esses valores em K grupos e retorna o grupo o qual aquele valor pertence.
No exemplo abaixo podemos ver a utilização da classe KBinsDiscretizer utilizando o algoritmo k-means para discretizar.
disc = KBinsDiscretizer(n_bins=10, encode='ordinal',
strategy='kmeans')
lot_kbins = disc.fit_transform(train[['LotFrontage']])Tratamento de outliers
Winsorizer
O método Winsorizer é um pouco diferente do trimming mostrado na última postagem, pois ele não exclui os valores com outliers, apenas substitui pelo valor máximo ou mínimo determinado, podendo estes ser com desvios padrões ou quantis.
cols = train.select_dtypes('number').columns.tolist()
w = Winsorizer(distribution='gaussian', variables=cols)
train_w = w.fit_transform(train)Engenharia de Atributos ao Cubo
Falou, galera, espero que tenham gostado do conteúdo sobre Engenharia de Atributos com Python. Sendo assim, para ver todos esses exemplos e executá-los, basta entrar no nosso Github.
Referências de Engenharia de Atributos
Conteúdos ao Cubo
Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.
- Machine Learning com ML.Net no Jupyter Notebook
- Análise Exploratória com ML.Net e Jupyter Notebook no Ubuntu
- ML.Net – Modelos em Produção com WebApi e Docker
- AutoML (Automated Machine Learning) com ML.Net
- Analisando Dados do Brasileirão Série A
- Estruturas de Dados em Python
- Extrair Dados da API do Cartola FC
- Organização de Arquivos e Pastas com Python
Então, finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades.

Programador e cozinheiro. Formado pela Universidade Federal do Piauí e com um mestrado (interrompido) pela UFRGS. Com uma grande sede de conhecimento, está sempre se perguntando os porquês e tentando dar o melhor naquilo que faz. Desde pequeno diz que vai ser cientista, seja da computação, de dados ou na cozinha. O conhecimento é a única esperança.
“Um homem não é outra coisa senão o que faz de si mesmo.” Sartre


