Fala galera do mundo dos dados, hoje falaremos de uma outra biblioteca Python para análise de dados o Numpy. Essa lib vai auxiliar na missão de entender a álgebra linear, que é o estudo dos vetores e regras para manipular esses vetores. Ela desempenha um papel muito importante na Ciência de dados, principalmente no Aprendizado de Máquina. A maioria conhece os vetores que são representados com uma setinha em cima (tipo ![]() ), mas esses vetores são na verdade os chamados vetores geométricos. Portanto nessa postagem nós vamos discutir um conceito mais genérico da Álgebra Linear utilizando o NumPy para exemplificar.
), mas esses vetores são na verdade os chamados vetores geométricos. Portanto nessa postagem nós vamos discutir um conceito mais genérico da Álgebra Linear utilizando o NumPy para exemplificar.
Vetores e matrizes
No geral, vetores são objetos especiais que podem ser adicionados entre si e multiplicados por escalares para procurar outro vetor. Assim, de um ponto de vista abstrato, qualquer objeto que satisfaça essas propriedades pode ser considerado um vetor. Dessa forma vetores geométricos, polinômios, sinais de audio e elementos de ![]() (tuplas de n números reais) são tipos de vetores.
(tuplas de n números reais) são tipos de vetores.
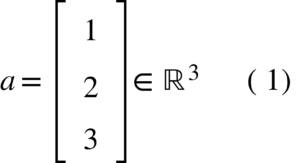
Porém, hoje nós vamos focar nessa última, que é a representação de vetores (e matrizes) que o Numpy utiliza. Por exemplo, a equação 1 mostra um vetor utilizando essa concepção:
Opa, mas e essas tal matrizes? Ah é… as matrizes são vetores bidimensionais, e os tensores são a generalização disso tudo (eles tem ordem n, se n for 0 é um escalar). Assim como está representado na figura abaixo de forma gráfica a diferença entre escalares, vetores, matrizes e tensores.
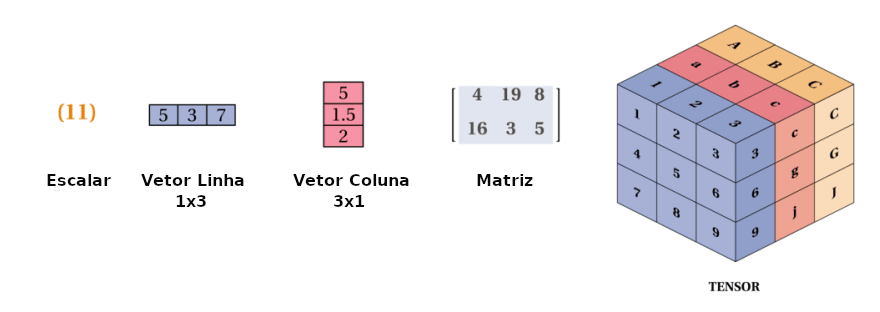
A seguir vamos falar das operações entre matrizes.
Adição de matrizes
Primeiramente, a adição de duas matrizes ![]() (A e B tem m linhas e n colunas) se dá da seguinte forma, elemento a elemento:
(A e B tem m linhas e n colunas) se dá da seguinte forma, elemento a elemento:
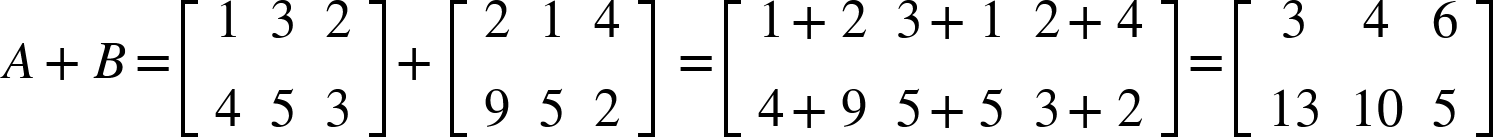
Mas, para realizar a operação, as duas matrizes precisam ter a mesma dimensão para ser efetuada a adição corretamente.
Agora vamos ver como implementar isso na linguagem de programação Python. A linguagem Python possui uma biblioteca chamada Numpy (np pros íntimos) que possui diversas funções matemáticas para trabalhar com vetores e matrizes.
Adição de matriz com Python
A operação de adição entre matrizes, no Numpy, é feito de modo semelhante, cria-se um vetor ou matriz com a função array do módulo numpy, depois é só somar que ele te retorna um array com o resultado. Antes de tudo é necessário importar o Numpy para utilizar suas funcionalidades. Assim como podemos observar o código abaixo:
import numpy as np a = np.array([[1, 3, 2], [4,5,3]]) b = np.array([[2, 1, 4], [9, 5, 2]]) a + b array([[3, 4, 6], [13, 10, 5]])
Multiplicação de matrizes
Dando continuidade as operações vamos ver a multiplicação, que é um pouco diferente. Quando multiplicamos uma matriz A de dimensões n x k por uma matriz C de dimensões k x m, o resultado é uma matriz n x m. Prestem muita atenção nisso, a dimensão das colunas de uma das matrizes tem que ser igual a dimensão das linhas da outra.
Assim como é importante notar também que AxC é diferente de CxA, caso seja possível executar as duas operações. Enfim, vamos ver na prática como ocorre, multiplicando e somando linha com coluna:

Igualmente na adição, vamos ver como realizar a multiplicação no numpy.
Multiplicação de matriz com Python
No numpy, pode-se utilizar a função dot para efetuar essa multiplicação. Caso utilize a*b (apenas para matrizes de mesma dimensão), a função vai te retornar o produto elemento a elemento. Assim podemos observar o código abaixo:
import numpy as np
a = np.array([[1, 3, 2], [4,5,3]])
c = np.array([[1,1],[2,3],[5,4]])
np.dot(a,c)
array([[17, 18],
[29, 31]])
np.dot(c,a)
array([[ 5, 8, 5],
[14, 21, 13],
[21, 35, 22]])
a*b
array([[ 2, 3, 8],
[36, 25, 6]])
a*c
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (2,3) (3,2)Na operação a*c por exemplo, é demonstrado que não é possível multiplicar elemento a elemento matrizes de diferentes dimensões, conforme falamos anteriormente. A seguir vamos ver a operação de multiplicação com um escalar.
Multiplicação de uma matriz por um escalar
A multiplicação de uma matriz por um escalar (um único número) vai retornar a multiplicação de cada elemento por esse escalar. No numpy é utilizado o asterisco para fazer essa operação (*).
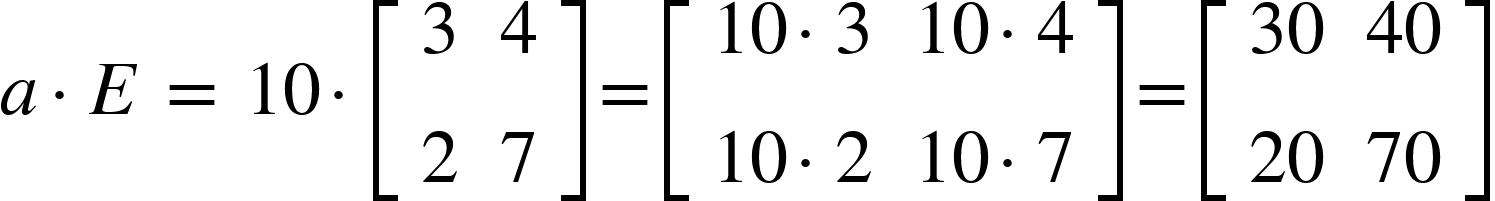
Assim vejamos abaixo a implementação dessa operação:
import numpy as np
c
array([[1, 1],
[2, 3],
[5, 4]])
10*c
array([[10, 10],
[20, 30],
[50, 40]])Posteriormente vamos ver operações específicas para matrizes, a inversa e a transposta.
Inversa e Transposta
Matriz inversa
A inversa de uma matriz ![]() é tal que AB = I = BA, onde I é a matriz identidade, que consiste numa matriz n x n e a diagonal principal (onde i = j , dado Aij) é igual a 1 e os outros elementos são igual a zero.
é tal que AB = I = BA, onde I é a matriz identidade, que consiste numa matriz n x n e a diagonal principal (onde i = j , dado Aij) é igual a 1 e os outros elementos são igual a zero.
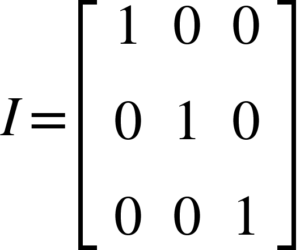
É importante salientar que nem todas as matrizes tem uma inversa, e quando tem ela é única. Dessa forma um dos métodos para calcular a inversa é a Eliminação de Gauss.
Eliminação de Gauss
Na eliminação de Gauss, alguns métodos são utilizados para transformar a matriz dada na matriz inversa. Isso é feito tentando transformar a matriz dada na matriz identidade e fazendo essas alterações na matriz identidade (que virará a inversa).
Esses métodos são:
- Trocar duas linhas entre si.
- Multiplicar todos os elementos de uma linha por uma constante não-nula.
- Substituir uma linha pela sua soma com um múltiplo de outra.
Por fim para verificar que o valor é mesmo a inversa, é só calcular ![]() e verificar que é igual à matriz identidade (I). Assim como podemos ver no exemplo abaixo:
e verificar que é igual à matriz identidade (I). Assim como podemos ver no exemplo abaixo:
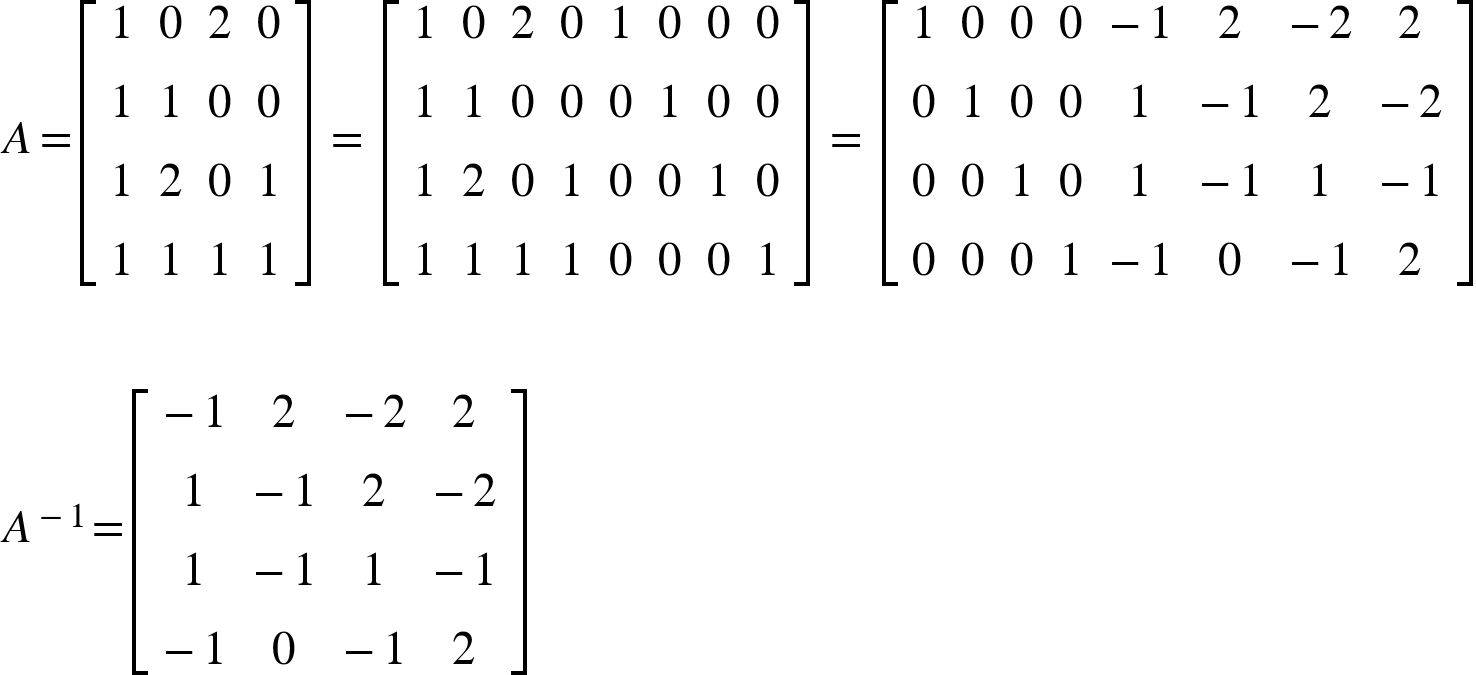
Assim como podemos as mesmas operações com o numpy, vejamos:
Matriz inversa com Python
Em numpy, se calcula a inversa com o método inv da biblioteca numpy.linalg. E para se conseguir a matriz identidade basta usar o método eye, passando a dimensão da matriz identidade n x n. Dessa forma podemos observar o código abaixo:
import numpy as np
d = np.array([[3,2],[3,4]])
np.linalg.inv(a)
array([[ 0.66666667, -0.33333333],
[-0.5 , 0.5 ]])
np.eye(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])Por fim vamos ver a matriz transposta e sua implementação com o numpy.
Matriz transposta
A matriz transposta ![]() é obtida trocando as linhas e colunas de lugar. Então a transposta de uma matriz 3×2 é uma matriz 2×3. Também é importante notar que a diagonal principal se preserva (no que podemos chegar na conclusão que a transposta da identidade é a própria identidade).
é obtida trocando as linhas e colunas de lugar. Então a transposta de uma matriz 3×2 é uma matriz 2×3. Também é importante notar que a diagonal principal se preserva (no que podemos chegar na conclusão que a transposta da identidade é a própria identidade).
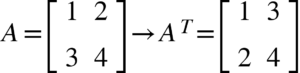
Para usar a transposta basta usar o atributo T do próprio array do NumPy.
Matriz transposta com Python
Assim como podemos ver no código abaixo a aplicação da matriz transposta com Python:
import numpy as np
d
array([[3, 2],
[3, 4]])
d.T
array([[3, 3],
[2, 4]])Álgebra Linear com NumPy ao Cubo
Para finalizar e não ficar só nesse bla bla bla teórico (que também é muito importante!), como resultado do estudo, segue um notebook implementando essas funções e alguns exemplos de slices (fatiamento): Algebra Linear com Numpy
Bem, por hoje é só, espero que tenham gostado. Saibam que álgebra Linear é beeeem mais que isso , mas quis aqui mostrar uma parte prática utilizando o NumPy. Se tiver qualquer crítica ou sugestão deixe um comentário aí embaixo! Até a próxima!
Referências de Álgebra Linear com NumPy
Para se aprofundar no assunto de Álgebra Linear
- Álgebra Linear – Khan Academy
- Mathematics for machine learning: Linear Algebra – Coursera
- Matrix Inverse
- Matriz transposta
Conteúdos ao Cubo
Por fim, deixo algumas sugestões de conteúdos que você pode encontrar no Dados ao Cubo, sempre falando sobre o mundo dos dados.
- Geometria Analítica com SymPy
- Estatística Descritiva Univariada
- Análise Exploratória de Dados com Python Parte I
- Análise Exploratória de Dados com Python Parte II
- Bem Vindos ao Dados ao Cubo: Uma Introdução a Ciência de Dados
- Variáveis em Python
- Extrair Dados da API do Cartola FC
- Web Scraping e Coleta de Dados Automatizada com Python
Finalizo com um convite para você ser Parceiro de Publicação Dados ao Cubo e escrever o próximo artigo, compartilhando conhecimento para toda a comunidade de dados. Não esqueça de assinar a nossa Newsletter para ficar por dentro de todas as novidades.

Programador e cozinheiro. Formado pela Universidade Federal do Piauí e com um mestrado (interrompido) pela UFRGS. Com uma grande sede de conhecimento, está sempre se perguntando os porquês e tentando dar o melhor naquilo que faz. Desde pequeno diz que vai ser cientista, seja da computação, de dados ou na cozinha. O conhecimento é a única esperança.
“Um homem não é outra coisa senão o que faz de si mesmo.” Sartre


